Глава 2: Обучение и эволюция

Выживание

Быть во времени
Надеюсь, я смог вас убедить, что жизнь по своей сути является вычислительным процессом, хотя мы лишь слегка коснулись того, что она на самом деле вычисляет. Минимальная функциональность для динамически стабильной формы жизни — это, конечно, репликация или, точнее, самостроение. Открытая эволюция требует конструктора фон Неймана, который, в свою очередь, является полноценной машиной Тьюринга. Конструктор позволяет создавать сложные и рекурсивные структуры, такие как ветви дерева или кровеносная система животного.
Но среды, в которых происходят строительство и репликация, совершенно не похожи на чистые сеточные миры клеточных автоматов фон Неймана. Реальный мир беспорядочен, постоянно меняется и вторгается в жизнь. Чтобы сохранить хоть какую-то целостность в таком мире, вычислительной системе нужна защитная граница.
Тем не менее, граница не может быть абсолютной, потому что жизнь никогда не может быть самодостаточной: вычисление требует энергии, а самостроение — материи.
Выходы также необходимы, поскольку ни вычисление, ни рост не могут быть абсолютно эффективными. Вычисление генерирует тепло, которое должно куда-то деваться. И не каждый атом, попадающий в живую систему, может стать ее функциональной частью. Поскольку материя и энергия не могут быть созданы или уничтожены, организму необходимо избавляться от материи (экскреция) и энергии (тепловые потери). Как вихрь, жизнь представляет собой динамический паттерн, который может существовать только в потоке более крупной среды.
Таким образом, тот вид вычисления, который мы называем «интеллектом», возникает из необходимости жизни взаимодействовать с окружающей средой. Эта среда неизменно включает в себя другие формы жизни, открывая двери для более высоких уровней симбиоза, о которых будет рассказано позже в книге. Здесь же мы исследуем интеллект в его самой простой форме: в одиночном режиме.
Представьте себе простую одноклеточную форму жизни — скажем, бактерию. Ее клеточная мембрана отделяет «я» внутри от внешнего мира. Но, как уже упоминалось, это отделение не может быть полным.

Усыпанные порами и ионными насосами, способные поглощать питательные вещества и выводить отходы, клеточные мембраны избирательно проницаемы для материи и энергии — так же, как и наши тела.

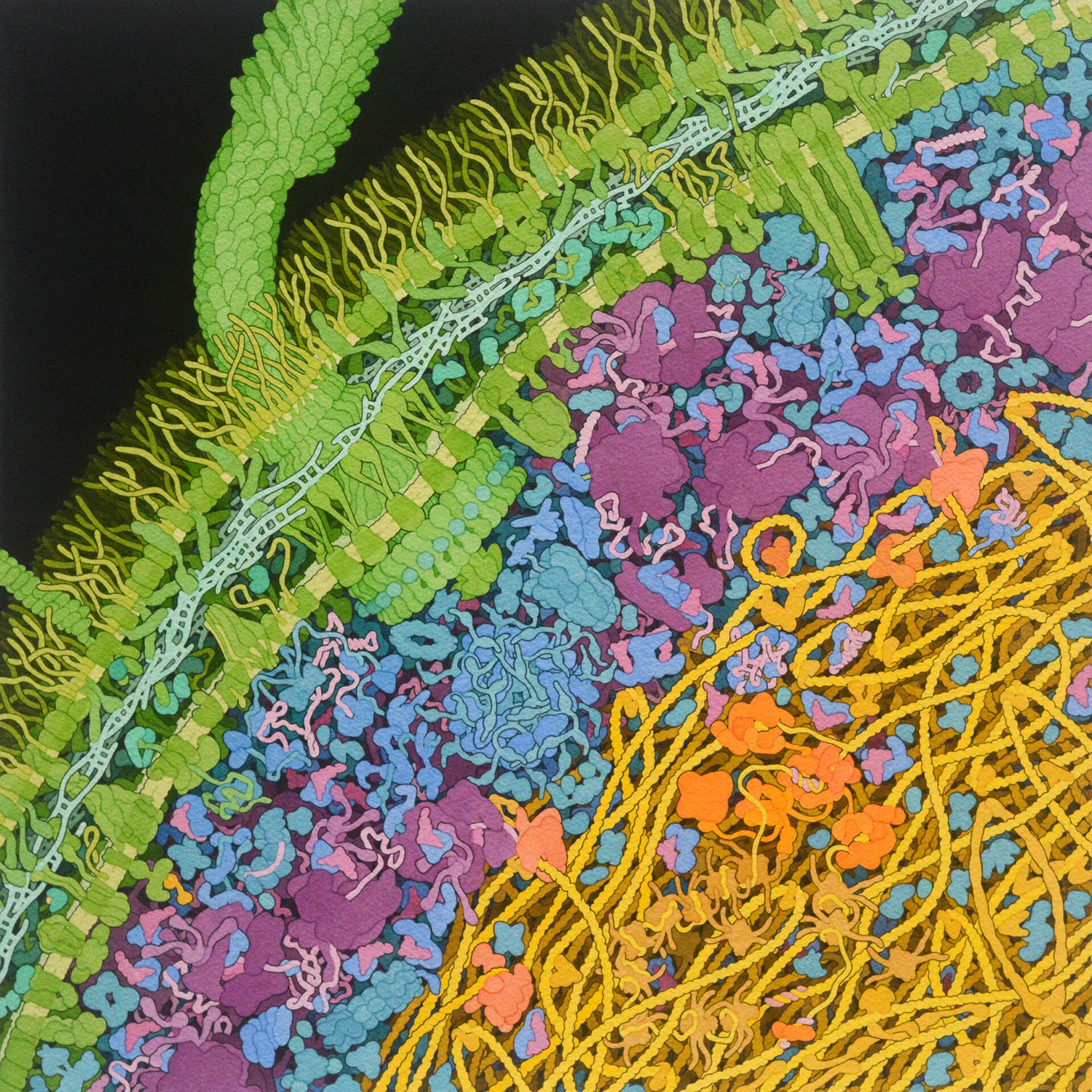
Иллюстрация молекулярного механизма внутри бактерии E. coli, Дэвид С. Гудселл, RCSB Protein Data Bank, 2021

Это также делает их проницаемыми для информации, ведь материя и энергия не являются универсальными. Калиевый ион не заменим на кальциевый, а красный фотон не равен ультрафиолетовому. Эти входные данные будут оказывать различное воздействие на организм. Таким образом, каждый вход также является, по сути, своего рода сенсором. Учитывая важность сенсорной информации для выживания организма, некоторые входы эволюционировали, чтобы быть в первую очередь информационными. Например, рецептор может «вкусить» молекулу, не пропуская её через мембрану. Главное — собрать информацию.

Чтобы обработать эту информацию, у бактерии есть нечто вроде «мозга». Он представляет собой динамическую сеть взаимодействующих генов и белков, которые подвержены влиянию сенсорных данных и могут контролировать клеточные процессы и поведение. Этот биохимический «мозг» также получает данные изнутри клетки, такие как метаболическое состояние и доступная энергия, позволяя внутренним состояниям, таким как «голод», модулировать поведение.

Некоторые бактерии могут плавать, используя винтообразный пучок моторизованных филаментов, называемый «жгутик» — хотя управлять движением в привычном смысле невозможно. Из-за простоты строения бактериального тела, незначительности силы тяжести и молекулярного воздействия, характерного для жизни в воде на таких малых масштабах, клетка не может различать лево и право, вверх и вниз. Плавая, она может лишь «бежать», вращая свои жгутики по часовой стрелке, чтобы двигаться вперед, или «крутиться», запуская некоторые из своих жгутиковых моторов в обратном направлении и заставляя клетку в целом вращаться хаотично, случайным образом меняя своё положение.

Классическая серия исследований биофизика Говарда Берга и его коллег в 1970-х годах показывает, как бактерии, просто чаще вращаясь, когда концентрация пищи падает, и реже, когда она растет, в среднем плывут к местам с более высокой концентрацией пищи — это поведение известно как «хемотаксис». Они могут использовать тот же подход, чтобы плыть к теплу («термотаксис») или, для фоточувствительных бактерий, к свету («фототаксис»).

▶ Хемотактические бактерии E. coli, плывущие к кристаллу сахара

Однако бактерия не может напрямую измерять концентрацию, температуру или уровень света, не говоря уже о различиях в этих свойствах вдоль своего микроскопического тела. Она слишком мала. По сравнению с любыми значимыми характеристиками окружающего мира бактерия является точечным объектом; можно почти сказать, что она существует только во времени, а не в пространстве. То есть она воспринимает жизнь как последовательность событий, и все, что она может узнать или наблюдать о своем пространственном окружении, может быть выведено только из этой последовательности событий.

Эти события все дискретны или «цифровы», даже когда они относятся к непрерывным физическим величинам, таким как химическая концентрация — потому что на бактериальном уровне химические вещества воспринимаются только по одной молекуле за раз, когда они присоединяются и отсоединяются от рецепторов на клеточной мембране. Поглощение фотонов и химические события, зависящие от температуры, также квантизированы.

Хотя эти дискретные события по отдельности случайны, окружающая концентрация, температура или освещенность определяют скорость их возникновения. Следовательно, номинально непрерывную переменную, такую как концентрация, можно оценить только путем подсчета таких молекулярных событий присоединения в течение определенного временного интервала, эффективно вычисляя скользящее среднее. Если бактерия плывет, и концентрация варьируется в пространстве, то в процессе оценки необходимо сделать статистический компромисс. Более длительный подсчет позволяет более точно оценить концентрацию, но ценой этого является сглаживание изменений во времени (или, эквивалентно, в пространстве).

Бактерии умело справляются с этой дилеммой, адаптируя свою стратегию оценки концентрации к конкретной ситуации.
Давайте подробнее рассмотрим, как работает процесс оценки.

Средний Бэттинг

С точки зрения бактерии, химическая концентрация — это текущая оценка вероятности будущих встреч с молекулой, основанная на истории прошлых встреч с ней. Если говорить более техническим языком, пусть последовательность молекулярных встреч обозначается как ( X ), тогда концентрация представляет собой изменяющуюся во времени оценку вероятности ( P(X) ).

Если эта математическая нотация вызывает у вас дискомфорт, позвольте мне попытаться компенсировать это, предложив аналогичную ситуацию из другой области: бейсбол.

Аарон с «Милуоки Брэйвс» в 1960 году

Вот мое наивное понимание самой известной статистики в спорте — среднего бэттинга. Каждый раз, когда бейсболист выходит на биту, он может либо добиться успеха, что мы можем представить как единицу, либо потерпеть неудачу, что можно обозначить нулем. Успех часто заключается в том, чтобы ударить по мячу, но, как оказывается, некоторые способы удара не учитываются, а другие, вроде «жертвенника», на самом деле не являются неудачами? (Если бы я не пронес в тайне научно-фантастический роман на тот единственный бейсбольный матч, на который меня потянули мои американские родственники, когда мы переехали в США, возможно, я бы узнал об этом раньше.) В любом случае... Со временем историю бэттинга игрока можно представить в виде последовательности единиц и нулей, где каждый раз, когда он на бите, создается один бит. Пропорция единиц — другими словами, среднее значение всех этих единиц и нулей — и есть средний бэттинг игрока.

Мы можем более внимательно изучить данные, поскольку бейсбольные фанаты выложили в интернет полные истории бэттинга игроков Главной Лиги Бейсбола (MLB), начиная с многих десятилетий назад.
Рассмотрим Генри «Хэнка» Аарона, которого широко считают одним из величайших игроков всех времен.

На протяжении своей долгой карьеры в Главной лиге бейсбола, с 1954 по 1976 год, Хэнк Аарон выходил на биту более двенадцати тысяч раз, и в 30,5% случаев ему удавалось успешно ударить по мячу и выйти на базу или лучше. Этот средний показатель «.305» считается впечатляющим.

Однако ни у одного игрока производительность не остается постоянной с течением времени. Это легко увидеть, если рассчитать средние показатели за отдельные сезоны (продолжительностью шесть месяцев каждый год, с апреля по сентябрь). Мы можем заметить, что в первые годы карьеры Аарона его средний показатель увеличивался, достигая пика более .350 в 1959 году. Как и в любом другом деле, в бейсболе есть кривая обучения.

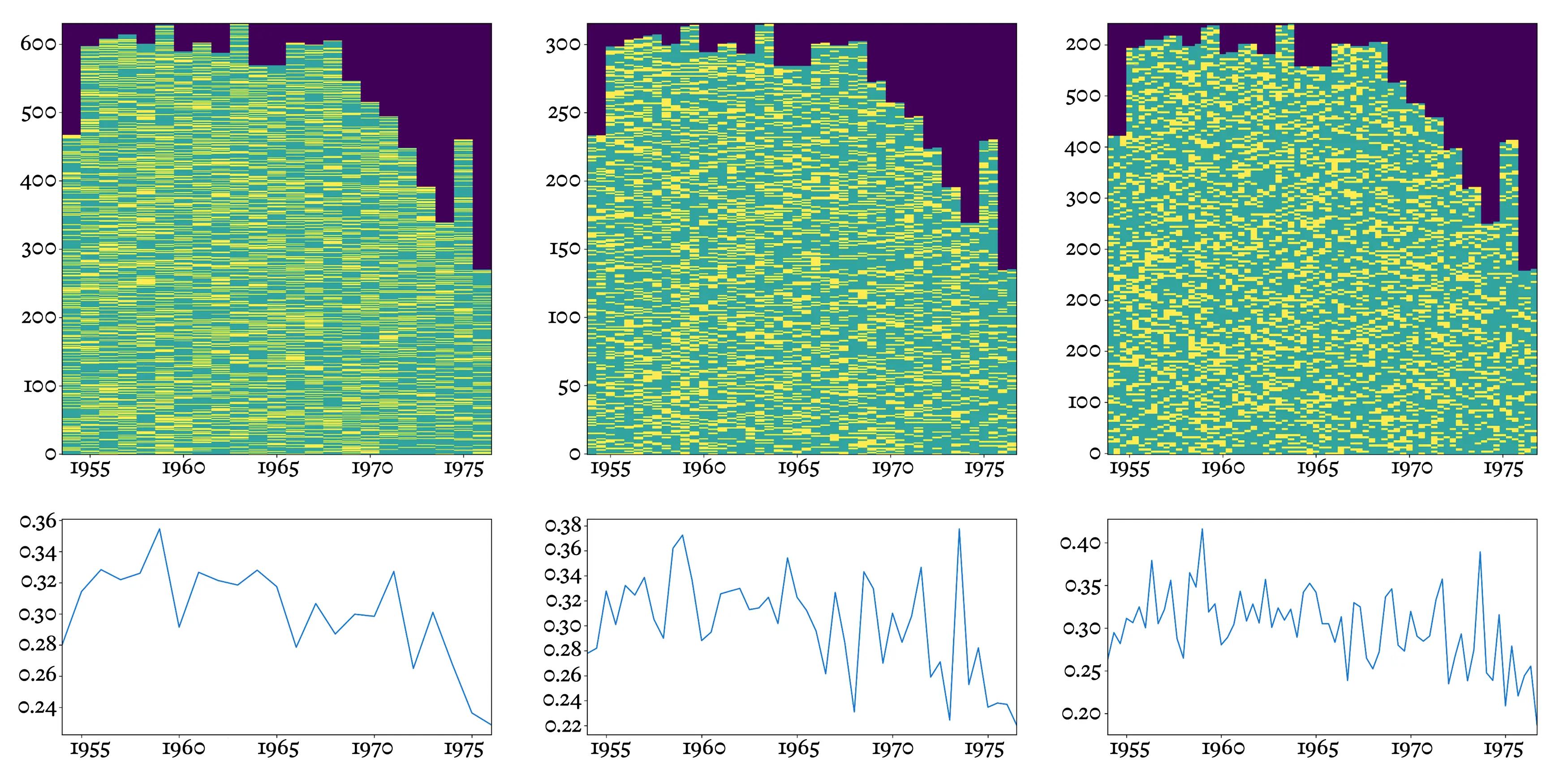
Полная история ударов Хэнка Аарона (верхний ряд) и средние показатели (нижний ряд), разбитые на 6-месячные интервалы, охватывающие полный бейсбольный сезон (левый столбец), 3-месячные интервалы (средний столбец) и 2-месячные интервалы (правый столбец).

Но, увы, тела стареют, и мелкие травмы накапливаются. Его производительность начала снижаться, сначала постепенно, затем более резко; к концу карьеры он стал бить ниже .250. К тому времени он выходил на биту лишь в половину случаев — безусловно, потому что менеджер внимательно следил за средними показателями, и по мере их снижения Аарон все чаще оставался на скамейке запасных.

Мы перешли от рассмотрения карьерных средних к средним показателям за шесть месяцев, но ничто не мешает нам усреднять данные за более короткие интервалы — три месяца, два месяца или даже один месяц. Этот более детальный анализ открывает новую информацию, до определенной степени. Используя трехмесячные интервалы, мы можем увидеть, что Аарон достиг своего карьерного пика всего за несколько лет до завершения карьеры, averaging an amazing .378 между июлем и сентябрем 1973 года. (В том году он завершил сезон с 713 хоум-ранами, всего на один меньше мирового рекорда, установленного в 1935 году Бэйбом Рутом. Тысячи писем к Аарону поступали, некоторые от поклонников, другие полны ненависти и угроз, от тех, кто был в ужасе от перспективы того, что чернокожий человек побьет самый священный рекорд бейсбола.)

Тем не менее, со временем не только средний показатель Аарона стал ниже; его выступления также стали более непредсказуемыми. Хотя высокие достижения по-прежнему оставались высокими, они чередовались с более низкими и непредсказуемыми результатами. Таким образом, короткий период усреднения, который в начале карьеры Аарона был бы весьма предсказуемым, позже стал менее информативным.

Часть этого эффекта объясняется простым недостатком данных. Когда мы усредняем за более короткие интервалы или Аарон выходит на биту реже, оценка становится менее точной, так как данных для усреднения становится меньше. В предельном случае, если наш интервал сократится до одной единственной попытки, «среднее» сможет принимать только два значения: 0.000 или 1.000, что делает его бесполезным для прогнозирования будущих результатов. Очевидно, что существует идеальный размер окна усреднения: достаточно большой, чтобы накопить приемлемую статистику, и достаточно маленький, чтобы фиксировать изменения со временем. Идеальный размер окна будет зависеть не только от частоты выходов на биту, но и от того, как часто происходят попадания, а также от стабильности игрока.

Все это говорит о том, что если X — это последовательность дискретных событий в прошлом, будь то попадания бейсбольного игрока или встречи молекул пищи с бактерией, P ( X ) сглаживает эти дискретные события в непрерывно изменяющуюся среднюю скорость, используя окно усреднения подходящего размера, которое также является оценкой вероятности столкновения с таким событием в ближайшем будущем. Хотя эта величина описывает прошлое, она является предсказательной моделью. Если в течение некоторого времени не происходило событий, вероятность низка; если только что началась череда событий, вероятность высока; если скорость увеличивается, то хорошая оценка будет выше исторического среднего, а если скорость снижается, то хорошая оценка будет ниже.

Так что, являются ли средние показатели бит (баттинговые средние) «реальными»? Очевидно, что средний показатель Хэнка Эйрона не измерял какую-то физическую величину в мире, в его теле или разуме — хотя он и не был свободен от физики мячей и бит, психологии питчеров или физиологии стареющих тел. У него не было единственного истинного значения, поскольку его можно было оценивать разными способами и на различных временных масштабах — хотя некоторые оценки лучше других в том смысле, что они более предсказуемы. Несмотря на свою неопределенность, баттинговые средние важны для игроков, тренеров и болельщиков, поскольку они как предсказывают, так и влияют на будущее.

То же самое касается статистических измерений, которые важны для бактерий. Как и бильярдные шары, молекулы — это дискретные объекты, подчиняющиеся микроскопическим физическим законам, которые не требуют макроскопических понятий, таких как «концентрация» или «температура». Но если бактерия хочет предсказать вероятность встречи с пищей, ей необходимо оценить концентрацию на основе зафиксированных событий, что-то вроде бейсбольных ударов.

Как описано в главе 1, развитие термодинамики Больцмана — например, Закон идеального газа — определяет такие величины, как давление, температура и концентрация, используя математические модели и приближения того же рода. Эти модели также включают подсчет молекул или событий в пределах временного окна или пространственного объема.

Приборы, такие как термометры или индикаторы pH, делают то же самое, используя экспериментальные установки, а не теорию. То же самое делает цифровая камера, подсчитывая фотоны, поглощаемые каждым пикселем. Короче говоря, как и баттинговые средние, такие переменные, как яркость, температура, pH и концентрация, зависят от моделей: способов предсказания будущих явлений на основе прошлой статистики.

(Нет) вещей самих по себе

Мы можем либо прийти к выводу, что такие свойства, как температура, не являются «реальными» — путь, который в конечном итоге ведет к солипсистскому отрицанию того, что что-либо является «реальным» — либо мы можем переосмыслить, что значит, чтобы что-то было реальным.

За пределами чистой математики «реальность» редко поддается полному определению. Мы видели, как концепция «температуры» теряет смысл, когда мы задаем вопросы о том, насколько горячий или холодный является среда, когда ее давление или плотность стремятся к нулю, где усреднение становится ненадежным. Поэтому, если нам задают вопрос вроде «Какова температура космического пространства?», мы должны ответить на него, задав дополнительные вопросы. Это о том, какова температура солнечной панели спутника? (Ответ: это полностью зависит от того, в какую сторону она направлена относительно ближайшей звезды и от теней любых близлежащих луны или планет.) Или речь идет о том, насколько комфортно будет вашей руке, если она будет подвергнута воздействию космоса? (Ответ: не делайте этого.) Для бактерии, адаптированной к водной среде, эти вопросы просто не имеют значения. Можно так же спросить человека: «Каков вкус нейтронной звезды?»

Как и вкус, температура не является «вещью сама по себе». Она не предшествует какому-то не наблюдаемому вселенной образом. Скорее, это модель, зависящая от наблюдателя, полезность которой, с точки зрения наблюдателя, зависит от ее предсказательной силы, имеющей значение для поведения. Это верно не только для температуры, но и для всех макроскопических явлений, которые нас интересуют и которые мы описываем с помощью языка, таких как «музыкальная нота», «стул», «бактерия» или «человек».

Это может быть верно даже для таких явлений, как «электрон», но здесь мы сталкиваемся с ограничениями в нашем понимании фундаментальных законов вселенной. «Электрон» может быть просто названием, которое мы присваиваем определенному виду распространяющегося возмущения в квантовом поле, или он может иметь какую-то более фундаментально «цифровую» природу, которую физики, исследующие основы реальности, могут однажды открыть.

А сами квантовые поля «реальны»? Кто знает?

Реальны ли электроны, фотоны, кварки и различные связанные с ними элементарные силы, являются ли они независимыми от наблюдателя «вещами сами по себе», или же более высокие объекты и характеристики, такие как температура, давление, стулья и столы, бактерии и люди, на первый взгляд, кажутся лишь идеями или «эпифеноменами». Наблюдаемая вселенная не заботится о таких идеях; в конце концов, продолжение существования стула не зависит от того, есть ли кто-то, кто воспринимает этот набор атомов как «стул». Атомы повсюду подчиняются бездумным законам физики.

«Игра жизни» математика Джона Конвея служит полезной иллюстрацией. Это не совсем игра, так как здесь нет игроков, счета, побед или поражений. Это просто набор правил, которые описывают, исходя из состояния игрового поля, каково будет его следующее состояние. (Это должно показаться знакомым. Игра Конвея на самом деле является самым известным примером клеточного автомата, хотя фон Нейман не дожил до её появления.)

Игра Конвея в тороидальном мире (т.е. верхний край соединяется с нижним, а левый — с правым), инициализированная произвольным шаблоном.

Правила просты:

Как пиксели или графическая бумага, мир состоит из сетки квадратных ячеек. Каждая ячейка может быть «живой» или «мертвой». Мы можем визуализировать эти состояния, закрашивая их черным (живой) или белым (мертвой).

На каждом временном шаге состояние каждой ячейки определяется состоянием этой ячейки и её восьми соседей на предыдущем временном шаге. Если ячейка живая, она останется живой только в том случае, если у неё есть два или три живых соседа. Если ячейка мертва, она оживает, если у неё ровно три живых соседа.

Согласно этим правилам, полностью мертвая доска останется мертвой навсегда; это так называемая «фиксированная точка» или «устойчивая стационарная ситуация». Как вы можете легко подтвердить с помощью ручки и бумаги, блок из 2×2 живых ячеек на в остальном мертвой доске также является устойчивым состоянием.

Конвей и его коллеги обнаружили, что простая "физика" Жизни может порождать множество интересных явлений более высокого уровня. Например, определенные конфигурации из пяти соседних живых клеток образуют стабильный четырехсостоящий циклический паттерн, который, кажется, движется по диагонали в пространстве, называемый "глайдером". Более сложная конфигурация клеток формирует "глайдерную пушку", в которой механизм, напоминающий поршень, выдает бесконечный поток глайдеров. Глайдерная пушка в Игре Жизни В Игре Жизни можно построить множество сложных машин, используя всего несколько простых элементов, таких как глайдеры и глайдерные пушки. На самом деле, было доказано, что, как и оригинальные клеточные автоматы фон Неймана, Жизнь является универсальным вычислительным устройством; несмотря на свою простоту, предприимчивый инженер может создать универсальный компьютер в Жизни. (В особенно впечатляющем проявлении рекурсивного увлечения, вычисления, необходимые для симуляции Жизни, были даже запрограммированы в самой Жизни! Это нужно увидеть, чтобы поверить.) Из этого следует, что, казалось бы, тривиальная вселенная Жизни может выполнять произвольно сложные вычисления, включая, возможно, симуляцию нашей целой вселенной. ▶ Жизнь, реализованная в Жизни, Филлип Бредбери, 2012 Как только система способна вычислять, ее основная физика становится несущественной для этих вычислений — помните, что, согласно Тьюрингу, все компьютеры эквивалентны. Поэтому так же справедливо утверждать, что вычисление не заботится о физике, как и говорить, что физика не заботится о вычислении. Это будет иметь значение для нас позже, так как позволяет нам понять функциональность в живой (или интеллектуальной) системе, не вникая в ее основные механизмы. Однако ярый физик может с полным основанием настаивать на том, что ни глайдеры, ни любые бесконечно сложные вещи, которые можно построить в Жизни, не являются "реальными" или "вещами сами по себе", в том смысле, что правила Жизни не включают такие объекты.

Существуют только мертвые и живые клетки, а также элементарные правила, определяющие их следующие состояния. Эти факты, и только они, составляют «Теорию всего» Жизни. Всё остальное — на усмотрение наблюдателя.

Однако, как наблюдатели, мы определенно можем видеть глайдеры. Они кажутся достаточно реальными. Что мы имеем в виду? Мы имеем в виду, что, если мы распознаем конфигурацию глайдера, мы можем сразу предсказать, что произойдет дальше: он будет проходить через четыре состояния и двигаться по диагонали, пока не наткнется на препятствие.

Если бы глайдер был единственным объектом на иначе пустой бесконечной доске, мы могли бы одним взглядом предсказать каждое будущее состояние всей доски на все времена. По сравнению с грубой вычислительной силой, необходимой для определения будущего состояния каждой клетки на доске, сэкономленные усилия… ну, бесконечны.

Таким образом, можно сказать, что глайдеры реальны только и исключительно потому, что, как концепция или модель, они полезны для предсказания будущего, когда возникает паттерн глайдера. Признание и понимание глайдеров позволяет проводить симуляцию без симуляции.

Нажмите, чтобы начать Игру жизни Конвея с добавленным «шумом» из микрофона (попробуйте похлопать)

Более того, паттерн глайдера имеет высокую значимость во вселенной Жизни, потому что он настолько прост, что возникает спонтанно. Это означает, что если мы представим себе, что Жизнь разворачивается на большой доске, где клетки время от времени случайно меняют состояние, глайдеры будут формироваться часто. И когда это произойдет, мы сможем немедленно предсказать их будущую траекторию — пока они не будут нарушены шумом или не столкнутся с чем-то.

Антропный принцип С точки зрения математика, паттерны, такие как глайдер и глайдерная пушка, являются особыми, поскольку они соответствуют «предельным циклам» — обобщениям идеи устойчивых состояний (таких как блок 2×2) до бесконечно повторяющихся циклов состояний.

Согласно квантовой теории поля, паттерны, которые мы называем «электронами», «фотонами» и «кварками», очень похожи на глайдеры: стабильные (хотя и колеблющиеся) решения основных уравнений поля, которые не определяют такие объекты явно. Это должно показаться знакомым: мы снова сталкиваемся с динамической стабильностью.

Если смотреть на это с этой точки зрения, глайдеры и элементарные частицы — это просто первые шаги в эволюционном процессе, согласно максиме, что всё, что существует, должно быть устойчивым (и наоборот, всё, что слишком динамически нестабильно, чтобы существовать... не существует).

Эволюция не обязана останавливаться на этом. Если восемь глайдеров столкнутся именно так, как нужно, они «реагируют», образуя глайдерную пушку.

И не только глайдерная пушка стабильна; она также создает больше глайдеров! Глайдерные пушки и несколько других простых объектов, которые могут возникнуть в результате столкновения глайдеров, являются основными ингредиентами для построения машины Тьюринга.

Синтез глайдерной пушки в игре «Жизнь» Конвея из восьми глайдеров

Может ли «Жизнь» Конвея привести к абиогенезу, так же как это делает bff? В нашем универсуме этот путь включал в себя первичные поля, сливающиеся в элементарные частицы, электроны и протоны, объединяющиеся в атомы водорода, конденсацию звезд, создание все более тяжелых атомов через ядерный синтез, формирование планет и последующие события, описанные в начале первой главы.

Это может предложить решение давней загадки о том, почему наш универсум кажется так тонко настроенным для возникновения сложной жизни. Как писал физик Стивен Хокинг в «Краткой истории времени»: «Законы науки [...] содержат множество фундаментальных чисел, таких как величина электрического заряда электрона и соотношение масс протона и электрона. [...] Удивительный факт заключается в том, что значения этих чисел, похоже, были очень тонко настроены, чтобы сделать возможным развитие жизни».

Для Хокинга и многих других представителей физического сообщества наше существование является доказательством того, что существуют многие вселенные, ведь если бы была только одна, ее совместимость с жизнью была бы чудом... а физики не верят в чудеса. В "мультивселенной", где законы физики различаются между вселенными, наблюдение за тем, что наша вселенная кажется тонко настроенной для поддержания жизни, можно объяснить наблюдательным уклоном, известным как "антропный принцип": конечно, вселенная, которую мы наблюдаем, идеально подходит для жизни, потому что никто не мог бы наблюдать за гораздо большим числом стерильных вселенных. Утверждать, что нам "повезло" жить в этой вселенной, так же абсурдно, как и говорить, что нам повезло жить на Земле, а не на Марсе, или внутри Солнца, или в межзвездном пространстве — короче говоря, в любом из бесчисленных мест в космосе, непригодных для жизни.

Так называемый "слабый антропный принцип" определенно верен. На Марсе нет "несчастных" людей, потому что там нет людей вообще. Однако сделать шаг от загадочного наблюдения о жизнеспособной тонкой настройке физических законов к "сильному антропному принципу", утверждающему, что любые и все мыслимые законы физики должны действовать где-то, — это довольно смелый шаг. Физики должны быть насторожены к чудесам, но многие также испытывают дискомфорт от идеи мультивселенной, где существуют любые и все законы. Действительно ли это необходимо для объяснения нашего собственного существования?

Более экономное объяснение заключается в том, что фундаментальные правила нашей вселенной, подобно тем, что в игре "Жизнь" Конвея, позволяют осуществлять вычисления — что, очевидно, является гораздо более низким порогом, чем допускать жизнь в том виде, как мы ее знаем. Множественные вселенные могут существовать или не существовать, но в любом случае, возможно, наша не так уж и особенная.

Учитывая источник шума, простая логика динамической стабильности будет отбирать стабильные сущности, которые затем могут начать объединяться в прогрессивно более сложные динамически стабильные структуры: кварки в нуклоны, электроны и нуклоны в атомы, атомы в молекулы и так далее. Такие сущности можно понимать как «прототипы репликаторов», подверженные тенденции к увеличению сложности и вычислительных возможностей, описанной в главе 1.

Если бы правила были другими, «прототипы репликаторов» были бы иными, и программное обеспечение жизни оказалось бы на другом вычислительном субстрате. Возможно, кварки и электроны не были единственно жизнеспособным вариантом. На самом деле, даже при тех же самых правилах каждая эволюционная стадия предлагает расширяющееся меню возможностей. ДНК не является единственным возможным носителем информации, а аминокислоты — не единственными «кирпичиками Лего» для молекул, подобных белкам. Нет никаких оснований полагать, что вся жизнь на Земле должна полагаться исключительно на правозавитые сахара, в отличие от их зеркальных аналогов — левозавитых сахаров. Независимо от таких «просто так» выборов, конечный результат будет одинаковым: репликация, вычисление и жизнь.

Таким образом, Дарвин мог быть прав еще в одном отношении, когда писал об абиогенезе, что «можно было бы также подумать об origenе материи». Он шутил, но — почему бы и нет? Материя тоже могла эволюционировать.

Умвельт внутри

Описывая «Жизнь» Конвея, мы позволили себе взглянуть на игрушечную вселенную с точки зрения третьего лица, как бы с высоты птичьего полета. Но теперь давайте вернемся к бактерии, живущей в нашем собственном мире, точечной относительно своего обширного водного окружения, но внутри полной сложной молекулярной машины; технически безмозглой, но не лишенной интеллекта.

Мы видели, что «мозг» бактерии реализует адаптивный алгоритм для оценки химической концентрации, пока она плавает, и кажется естественным назвать эту измерение «целеустремленным», поскольку оно определенно выглядит так, будто цель состоит в том, чтобы есть и избегать токсинов — коротко говоря, выживать.

Я утверждал, что сама идея «концентрации» — это то, что бактерия, похоже, создает для достижения своей цели; химическая концентрация, используя термин пионера биологии Якоба фон Уэкселя, является частью umwelt бактерии: её «вселенной значимого».

Позже мы рассмотрим, как мощные социальные аспекты предсказательных моделей влияют на будущее, но сейчас давайте сосредоточимся на одиночной игре. Не трудно понять, почему бактерия заботится о своем «среднем показателе», о том, как часто она сталкивается с молекулами, которые может поглотить.

Насколько этот показатель может варьироваться и как низким он может быть, конечно, зависит от того, насколько истощены её запасы. Поэтому часть umwelt бактерии также включает её внутреннее состояние; давайте назовем это состояние H , что означает «скрытое». В общем, H включает «зону комфорта», окруженную «зоной опасности»; за пределами зоны опасности находится смерть. В самом простом случае, если предположить, что H представляет собой количество доступной пищи внутри клетки, оценка «индикатора здоровья» P ( H ) будет выглядеть как тот же процесс сглаживания, что и для оценки P ( X ), но теперь на основе дискретных внутренних метаболических событий H , а не измерений внешней среды X .

«Задача №1» организма — поддерживать свою внутреннюю оценку P ( H ) в зоне комфорта: это и есть «гомеостаз». Бактерия достигает этого через действия, которые мы также можем представить как набор дискретных моторных событий O (для «выхода»). Эти действия могут быть видимыми с наружи — например, реверсирование жгутиков для кувырка — или они могут быть внутренними, такими как включение или выключение гена или метаболического пути.

В любом случае, гомеостаз включает выполнение действий O в ответ на внешние наблюдения X , которые поддерживают H в пределах зоны комфорта. Это интеллект в его самой примитивной форме.

Общепринято считать, что здесь работает нечто вроде «обучения с подкреплением», позволяя организму учиться выполнять необходимые действия на основе обратной связи, которая может быть положительной («чувствовать себя более комфортно») или отрицательной («чувствовать себя менее комфортно»). Однако сама идея связывать возникновение интеллекта с обучением с подкреплением — или любым видом контролируемого обучения — подразумевает наличие оракула, который может выдавать награды и наказания или давать правильные ответы. Откуда взялся этот оракул? Как он стал умным? Возможно, такого оракула не существует!

Гораздо проще и обобщённее рассматривать эволюцию интеллектуального поведения как результат «неконтролируемого» обучения (или, как его сейчас иногда называют, самоконтролируемого обучения) совместного или «объединённого» распределения вероятностей P(X, H, O). Бактериальные популяции, которые учатся этому совместному распределению вероятностей, не только «знают», как оценить концентрацию питательных веществ и своё внутреннее состояние, но также, в определённых условиях, «знают», каковы будут последствия различных действий в разных внутренних и внешних обстоятельствах.

Критически важно, что это совместное распределение является предсказанием как самого себя, так и окружающей среды — и последствий для себя различных возможных действий. Совместное распределение включает в себя всё нижеуказанное «знание»:

Как понять, что ты голоден;
Как измерить концентрацию пищи;
Как твои следующие действия могут повлиять на будущую концентрацию пищи; и
Насколько меньше голодным ты будешь, когда получишь эту пищу.

Таким образом, совместное распределение содержит всё, что может понадобиться для «знания» о том, как вести себя, чтобы выжить — по крайней мере, в отношении пищи.

Далее я уберу кавычки вокруг «знать» и «знание». Я использовал кавычки по двум причинам. Одна из причин глубока, а другая — менее значима.

Глубокая причина связана с различием между пассивной, абстрактной моделью и реальным агентом, чьи предсказания включают действия, которые он предпринимает и которые определяют будущее. Я подробнее обсудю это чуть позже.

Термитники вдоль старой телеграфной линии на мысе Йорк, Австралия, 1983 год; то, как термиты строят эти впечатляющие сооружения, часто приводится в качестве примера «компетенции без понимания».

Но сначала давайте разберемся с более поверхностной причиной использования кавычек: различием, которое многие когнитивные ученые проводят между знанием и компетенцией. Фраза «компетенция без понимания» часто используется для описания того, как агент может действовать так, как будто у него есть знание, хотя, по всей видимости, этого знания у него нет.

Не будем говорить о бактериях; человеческие бейсболисты или гонщики на спортивных автомобилях обладают удивительной физической интуицией в своей области, но большинство бейсболистов не смогли бы объяснить или рассуждать о параболических траекториях в общем, а большинство гонщиков не знают уравнений трения или центростремительной силы. Так что, знают ли они физику или нет?

Это звучит как более глубокий вопрос, чем на самом деле является. Математика, физика и, в частности, способность объяснять вещи с помощью языка — это все навыки или компетенции сами по себе; ни один из них не вытекает из обучения тому, как махать битами, ловить мячи или водить гоночные автомобили — и наоборот. Множество «ботаников» достаточно хорошо знают физику, но так не разбираются в спорте, что им может понадобиться заглянуть в Википедию, чтобы узнать, что такое «средний показатель отбивания». (Спасибо, Википедия.) И, конечно, символическая математика и язык недоступны агенту с очень ограниченной вычислительной способностью бактерии, даже если такие агенты обладают почти математически совершенными компетенциями в какой-то практической области.

Скрытые Переменные

Как мы увидим в главе 8, символические навыки и способности, такие как язык и математика, также могут быть полностью представлены в виде совместных распределений вероятностей — хотя и огромных, сложных. Большинство из нас, кто знает физику и интуитивно понимает, как водить машину или бить по мячу, не связывают эти две области, но для некоторых людей математическое мышление и физические интуиции могут быть тесно связаны, так же как звук голоса и движение губ говорящего; в любом случае, всё это содержится в большом общем совместном распределении P(X, H, O).

Обучение

Эффективное обучение P(X, H, O) — то есть успешное его представление без исчерпывающего запоминания вероятности каждой отдельной комбинации обстоятельств, состояния и действия — требует сжатия данных. Без такого сжатия размер модели, даже для простого организма, такого как бактерия, был бы непрактичным; следовательно, обучение модели было бы очень сложным, а её хранение или оценка — дорогими.

Как мы уже видели, сжатие данных включает в себя поиск закономерностей в данных и их выделение. Для символических данных, которые обычно сжимаются «без потерь» с помощью алгоритмов, подобных тем, что используются для ZIP-архивов, такие закономерности, как правило, принимают форму повторяющихся последовательностей. Когда же данные непрерывные, а сжатие «с потерями», как в случае с MP3-аудио или изображениями JPEG, нахождение этих закономерностей позволяет игнорировать несущественные детали, выявляя меньшее количество значимых «скрытых переменных».

Для бактерии важными скрытыми переменными являются концентрации молекул, связывающихся с рецепторами. Чтобы понять, почему это так, представьте, что у бактерии есть сто рецепторов, которые связываются с каким-то интересующим химическим веществом, например, аспартатом (для E. coli это «вкусно»). Каждый рецептор может быть занят или незанят молекулой аспартата.

Предположим (я просто придумываю цифры), что занятость измеряется в миллионных долях секунды, и бактерия сталкивается с нуля до тысячи молекул аспартата в секунду, когда плавает. Поскольку состояние каждого рецептора можно рассматривать как двоичный разряд: 0 — для незанятого и 1 — для занятого, эти сто рецепторов создают поток информации, который составляет сто миллионов бит информации в секунду. Это много бит в секунду, примерно в десять раз больше, чем нужно для передачи 4K видео.

К счастью для маленького мозга бактерии, подавляющее большинство этой информации либо бесполезно, либо избыточно. Поскольку клетка так мала и нет значительных разниц в концентрации вдоль её длины, не имеет значения, какие рецепторы заняты — рецепторы «симметричны», и любое значение, которое можно извлечь из них, «инвариантно» к этой симметрии. Так что мы можем просто сложить все эти биты вместе.

Даже при сложении общая сумма почти наверняка будет равна либо 0, либо 1 в любой момент времени, потому что время занятости короткое, а концентрация низкая. Это означает, что мы уже снизились до всего лишь одного миллиона бит в секунду. Затем, когда мы учитываем, что точное время событий связывания не имеет значения — это означает, что существует «локальная временная симметрия» или инвариантность к точному времени событий связывания — мы понимаем, что можем просто складывать все единицы каждую секунду, что дает нам концентрацию как среднюю скорость занятости за одну секунду.

Таким образом, мы снова возвращаемся к усреднению по временным интервалам, как при расчете средней результативности. Это единственное число в секунду, которое можно представить всего лишь с помощью нескольких бит, охватывает подавляющее большинство реальной информации, поступающей через эти сто рецепторов, хотя немного больше информации можно извлечь, сделав окно усреднения адаптивным, как упоминалось ранее.

Эволюция, вероятно, отшлифовала что-то близкое к этой схеме сжатия, поскольку она отбирает полезную информацию и отбрасывает все остальное. Такое сжатие делает общую распределение P(X, H, O) обучаемым, потому что шаблоны, связывающие X с H и O , могут быть обобщены только если хаос несущественных деталей в X был устранен. В языке теории информации полезные части X — это «сигнал», в то время как отбрасываемые части — это «шум».

Помните, этот сигнал полезен именно потому, что он представляет собой непрерывную оценку вероятности будущего события стыковки — хотя стоит отметить, что эта непрерывная оценка сама по себе представлена как дискретные, стохастические сигналы внутри клетки, так что, называя это непрерывным числом, мы немного моделируем саму модель. Но мы забегаем вперед. Более важно то, что мы пришли к практическому определению химической концентрации, просто размышляя о том, что имеет значение для будущего бактерии, учитывая ее прошлое. Концентрация реальна, потому что она предсказуема, так же как температура в духовке реальна для вас, потому что знание о ней позволит вам предсказать, приготовится ли ваша еда или обожжет ли вас палец, если вы к ней прикоснетесь.

Голод в этом плане схож. Точно так же, как точная последовательность молекулярных взаимодействий, приведшая к определенной оценке концентрации, не имеет значения, так и точная последовательность энергозатратных действий, приведшая к истощенному энергетическому состоянию, не имеет значения; важно то, что смерть наступит без дополнительной пищи. Таким образом, голод «реален» в точно таком же смысле — и по той же причине — что и концентрация: оба являются полезными латентными переменными для эффективного моделирования P(X, H, O) . То, что одна из этих латентных переменных является оценкой условий за пределами клетки, а другая — оценкой условий внутри клетки, станет интересным, когда мы начнем рассматривать социальные отношения между клетками.

Но для нашей одинокой бактерии, пробивающейся в этом мире, нет никакой разницы.
Моделирование
До сих пор я утверждал, что моделирование единого совместного распределения вероятностей, P(X, H, O), достаточно для того, чтобы установить реальность как регулярных характеристик внешнего мира (таких как температура, концентрация и яркость), так и внутренней жизни организма (например, голода). Я не объяснил, как возникают такие модели и почему организмы с моделями кажутся целеустремленными.
Я также намеренно оставлял неопределенным слово «модель», колеблясь между его использованием как существительного и глагола. В качестве существительного мы часто воспринимаем модель как нечто безтелесное, возможно, алгоритм или набор уравнений, представленных в абстрактной форме. Одномерная линейная модель, например, может быть записана как f(x) = wx и полностью определяется единственным числом w.
Миллиарды параметров в большой модели, обученной с помощью машинного обучения, не отличаются — они просто занимают гораздо больше места для записи. В качестве глагола «моделирование» может означать обучение или приближение w (или, эквивалентно, миллиардов параметров, часто выраженных в виде гигантской матрицы «весов» w_ij между искусственными «нейронами» i и j) на основе обучающих данных; или это может означать оценку полученной модели, то есть фактический расчет f(x) для данного x.
Живой организм явно больше глагол, чем существительное; «глагольность» или, чтобы использовать более резонирующий термин, «агентность», именно это отличает живые существа от мертвых. Живые существа делают что-то по своей воле; неживые — нет.
Куча параметров, распечатанных на гигантском рулоне бумаги и запихнутых в шкаф, чтобы больше никогда не увидеть света, определенно не является живым существом. Это просто инертная материя… мертвая информация. (Похожим образом, как рулоны ДНК, все еще свернутые внутри клеток животного после его смерти.)

) Даже называть эти числа информацией может быть преувеличением, поскольку если нет читателя — никакого активного процесса, использующего эти напечатанные числа для выполнения чего-либо — они могут быть столь же бессмысленными, как и пустыми. Разницы не будет. Информация, как метко выразился антрополог и философ Грегори Бейтсон, — это «разница, которая имеет значение».

Существительное и глагольное значения слова модель отличаются друг от друга так же, как определение слова функция у математика отличается от определения у практического программиста. Для математика функция — это абстракция; она может быть непознаваемой на практике (например, четность или нечетность количества монет в обращении в любой данный момент) или даже принципиально невычислимой (например, правильность произвольного математического утверждения). Хотя они могут быть интересны в теории, для программиста такие «функции» — чепуха. Программистов интересуют только функции, которые можно реализовать, запустив реальный код, который может функционировать, или который, если в нем есть ошибки, не будет работать.

Связано с этим, помните, что O в P(X, H, O) означает «выход». Жизнь должна действовать (еще одно слово для «функционировать»). Живое существо — это процесс, а не распечатка или математическая абстракция; поэтому эти действия должны быть осуществлены — иначе процесс будет отключен от мира, и, с причинной точки зрения, модель может не существовать.

В так называемой «авторегрессивной последовательной предсказательной» настройке, используемой многими современными несупервизированными ИИ-моделями, обычно выполняется действие с максимальной вероятностью согласно P(X, H, O). В следующий момент времени выполненное действие, вместе с любыми новыми наблюдениями X и H, становится частью прошлого, и модель оценивается снова. Таким образом, каждое действие зависит не только от прошлых наблюдений, но и от прошлых действий. Организм, следовательно, моделирует себя совместно с окружающей средой и, таким образом, осуществляет агентное или «глагольное» моделирование. Он запускает свою собственную программу в непрерывном цикле.

Я выразил программу в виде вероятностного распределения, а не в более очевидной для программиста форме детерминированной функции, сопоставляющей входные данные с выходными, по двум причинам.

Во-первых, как мы уже видели, биологические вычисления являются стохастическими, поэтому действия следует рассматривать с точки зрения вероятностей, а не уверенности. Это также верно для моделей ИИ; при ненулевой температуре, как это обычно используется в чат-ботах, выполняемое действие выбирается из вероятностного распределения, а не полностью определяется входными данными. Во-вторых, эти действия не просто выходные данные, но и входные данные в следующий момент времени.

Уроборос (монстр, поедающий собственный хвост), изображенный в алхимическом трактате 1478 года

Здесь действует «странная петля». Поскольку модель является совместной, все чувства активны: действия зависят не только от внутренних и внешних восприятий, но и все восприятия зависят от действий. В нашем примере с хемотаксисом, например, любое воспринятое изменение концентрации питательных веществ и его интерпретация будут зависеть от того, плывет ли бактерия вперед или кувыркается на месте — что, в свою очередь, зависит от воспринимаемой концентрации питательных веществ. Более того, модель всегда моделирует саму себя в том смысле, что она предсказывает свои собственные будущие состояния и действия, помимо предсказания окружающей среды. Мы даже можем сказать, что она предсказывает свои собственные предсказания, в некоем бесконечном регрессе.

Жизнь — это зал зеркал.

Обучение через эволюцию
Активное моделирование, описанное выше, кажется, не оставляет места для обучения — только для действий или, на математическом языке, для оценки функции. Но откуда берется сама функция, которая постоянно оценивается, P(X, H, O)? Этот вопрос напоминает загадку абиогенеза, и это не случайно.

Еще в 1948 году Тьюринг осознал, что эволюцию можно понять как процесс обучения методом проб и ошибок.

Это может показаться грубым и неэффективным, но это необходимый старт для любого более сложного вида обучения. Всё, что учится, либо научилось учиться в процессе эволюции, либо было создано существами (пока что — людьми), которые сами научились учиться, эволюционируя.

▶ Симулированная популяция бактерий, обучающихся хемотаксису. Каждая бактерия движется (вверх, вниз, влево или вправо) или кувыркается (случайным образом меняя направление движения) в зависимости от функции своей сенсорной среды, определяемой её «геномом», представленным строкой пикселей справа. Бактерии получают «энергию» под вращающимся красным светом и теряют её в других местах. Если их энергия падает до нуля, они умирают, а если достигает порога, они делятся, реплицируя свой «геном». Со временем выживают только те бактерии, чьи «геномы» реализуют эффективную стратегию.

Предположим, у нас есть мир, в котором бактерии уже каким-то образом возникли; и если они выживут, они смогут размножаться, в процессе «клонируя» свои модели P(X, H, O), чтобы передать их дочерним клеткам. Мы предполагаем, другими словами, что P(X, H, O) закодирован генетически. В конце концов, если P(X, H, O) — это вычислимая функция, её можно реализовать с помощью кода, и поскольку бактерия является «самовоспроизводящим автоматом», как описывал фон Нейман, она уже содержит универсальную машину Тьюринга в коробке. Вычислительные ресурсы бактерии будут ограничены, и некоторые функции будет проще выразить на этой биологической платформе, чем другие, но теоретически любое вычисление возможно!

Благодаря генетическому кодированию, код также открыто эволюционируем. Он может улучшаться не только через утомительные, старомодные мутации, как у миллиона обезьян на миллионе печатных машинок, но и гораздо эффективнее через симбиоз, как описано в главе 1. Возможно, эволюция, во всей своей саморегулирующейся славе, не является такой уж медленной обучающей алгоритмической системой.

Так что же делает P(X, H, O) «более приспособленным»? Короче говоря, это тот, который более динамично стабилен.

В качестве первого приближения: Если высокая вероятность приписывается состоянию «мертв», то есть переходу из «опасной зоны» в «зону смерти», тогда модель, в самосбывающемся пророчестве, будет предсказывать — и предпринимать — действия, которые приведут к её собственной гибели. Однако более совершенная модель не будет совершать самоубийство. Она будет присваивать наивысшие вероятности «зоне комфорта», с уменьшающимися вероятностями за её пределами.

Если модель не точна, не последовательна или недостаточно универсальна — не предсказывает смерть, не учитывает связи между действиями и состояниями или свои собственные будущие действия, включая новые условия — тогда она будет менее эффективной, чем модель, которая точна, последовательна и универсальна, и, следовательно, лучше избегает состояний, ведущих к смерти.

Если доступны сигналы, будь то внутренние (H) или внешние (X), которые могут помочь в вышеупомянутых предсказаниях, то модель, способная использовать эти сигналы, будет более эффективной, чем модель, лишенная их. Поскольку моделирование (глагол) требует значительных вычислительных ресурсов (а значит, и энергии), меньшая, более компактная модель, которая предсказывает будущее так же хорошо, как и большая, окажется в выигрыше, потому что она будет реже испытывать нехватку ресурсов и оставит больше возможностей для воспроизводства.

В качестве бонуса, сжатие модели, как правило, идет рука об руку с универсальностью, что означает, что, при равных условиях, более компактная модель также с большей вероятностью продолжит хорошо работать в новых условиях.

Таким образом, в условиях ограниченных ресурсов организмы с постепенно улучшенными моделями P(X, H, O) будут превосходить тех, у кого модели хуже, и на протяжении многих поколений моделирование станет действительно эффективным.

Причина через следствие Термин «хороший», применяемый к модели, может быть истолкован по-разному. Для специалистов по данным «хорошая» модель обычно означает модель с низким уровнем ошибок на отложенных тестовых данных или ту, которая хорошо справляется с какой-либо заранее определенной задачей. Эта мера «хорошести» относится к модели (существительному), в отличие от динамичного агента, который моделирует (глагол).

Измерение "доброты" действительно требует вычислительной оценки — то есть, необходимо кратковременно "оживить" модель, сбросив её состояние, и многократно вычислить её реакцию на тестовые стимулы. Однако в таком искусственном контексте обычно отсутствует понятие времени или агентности, и "доброта" — это то, что говорит о ней специалист по данным. Это и есть крайне искусственная обстановка "обучения с учителем".

С другой стороны, модель, которая является "хорошей" с точки зрения эволюции, — это та, которая работает, или, по крайней мере, работает достаточно хорошо, что позволяет ей эффективно предсказывать будущее. Действуя как агент, она склонна способствовать осуществлению этого будущего: самосбывающееся пророчество обратной причинности.

Очевидный парадокс возникает из того, что причины должны предшествовать своим следствиям. Как можно сказать, что что-то происходит из-за своего следствия?

Тем не менее, в разговорной речи мы делаем это постоянно. Например, предположим, что я разговариваю с другом в кафе, затем взгляну на часы, вскочив, мчусь к выходу, оставив кофе недопитым. Сосед за столиком недоумевает, почему я так спешу на велосипеде. Мой друг говорит: "О, это просто потому, что он снова опаздывает в офис."

Это совершенно непримечательный обмен репликами... но если задуматься, это довольно странное употребление слова "потому что". Если камень катится с холма, готовый раздавить припаркованный автомобиль, и кто-то спрашивает, почему он это делает, могут быть всевозможные ответы. Возможно, произошел оползень выше, или он отломился от скалы. Мы не говорим, что он катится вниз по холму "потому что" внизу припаркованная машина. Причины находятся выше, в прошлом, а следствия — ниже, в будущем.

С этой точки зрения, следствие, предшествующее своей причине, кажется бессмысленным.

Однако, когда речь заходит о бактериях, людях и всем, что между ними, будущее, или его желаемая модель (в которой вы в безопасности, в тепле, сыты, с кофе в руках и успеваете в офис ровно вовремя), кажется, влияет на события, предшествующие ему, а не наоборот — события неумолимо определяют будущее.

На самом деле, с точки зрения эволюции, только те существа, чьи модели успешно предсказывают их собственное будущее, вообще имеют будущее! Конечно, ничего из этого не происходит в нарушение законов физики — но, как и сама жизнь (по Шредингеру), это определенно выглядит подозрительно. В детерминированной вселенной как может "план" или "намерение" повлиять на то, что просто произойдет? (Если вы думаете, что это похоже на парадокс свободной воли: да, это так. Мы к этому вернемся в главе 6.)

Ответ приходит из той странной петли, присущей авторегрессионному моделированию последовательностей. Мы уже видели, почему эволюция жизни подразумевает эволюцию "достаточно хорошей" модели P(X, H, O). Эта модель порождает действия в мире, но мир также порождает модель. Хотя модель может учиться только на прошлом, она является моделью, потому что может предсказывать будущее. Когда это предсказание влияет на ее действия, мы получаем нечто, что выглядит как обратная причинность. Чем мощнее модель — или, можно сказать, чем она "умнее" — тем более выраженным будет этот эффект.

Когнитивный ученый Терренс Дикон называет системы, демонстрирующие явную обратную причинность, "интенсиональными". Мы также можем назвать их "агентными", "целеустремленными" или, в широком смысле, "живыми". Таким образом, для камня, катящегося вниз по склону, автомобиль внизу может войти в "почему" вещей только если кто-то или что-то намеренно толкнул этот камень.

На этом этапе мы рассмотрели два аспекта, по которым модель можно назвать "хорошей". Для специалиста по данным модель "хороша" в той степени, в какой она показывает хорошие результаты на тесте.

Для живого организма модель считается «хорошей» в той мере, в какой она успешно предсказывает будущее — как мира, так и самого себя, а также последствия своих действий для себя и окружающего мира. Третий смысл «хорошего», связывающий эти два аспекта, является нормативным, а не описательным: модель хороша, если она сохраняет организм в живых, потому что жизнь — это хорошо, а смерть — плохо. Обратите внимание, что это нормативное качество возникает в эволюционном контексте без чего-либо, напоминающего обучение с подкреплением, при котором внешний оракул или учитель распределяет награды и наказания. На самом деле «наказание» отдельного организма в дарвиновских условиях невозможно, поскольку единственной негативной обратной связью является смерть, которая препятствует любому последующему обучению! Скорее, стремление к жизни возникает из некоего рода тавтологии: мертвые вещи не моделируют; живые — моделируют; их модели успешно предсказывают их собственную живость; следовательно, это «хорошо».

Добро и Истина

Хотя сама смерть является ничто, состояния, близкие к смерти, будут вызывать отвращение у любого существа, эволюционировавшего с учетом того, что смерть выступает в роли того, что физики называют «поглощающим граничным условием». Быть отвращенным к смерти, другими словами, — это способ не умереть. Отвращение приводит к действиям, которые, вероятно, отводят существо от «плохого» состояния и направляют его к более благоприятному для выживания. Эта нормативная оценка и реакция на нее одинаковы для бактерии, плывущей от токсического химиката, жука, убегающего от наступающей ноги, кролика, уклоняющегося от волка, или человеческого беженца, спасающееся от гражданской войны.

Как мы рассмотрим в главе 4, животным необходимо усваивать подобного рода нормативные сигналы в тот момент, когда они становятся многоклеточными. Они делают это, используя древние нейромодуляторные химические вещества, такие как дофамин и серотонин, которые впервые эволюционировали у плоских червей и остаются основой наших самых элементарных чувств, таких как желание и насыщение.

С нашими большими мозгами и сложными культурами человеческие представления о том, что такое «хорошо» или «плохо», стали многогранными и нюансированными, но все они восходят к этим эволюционным основам.

Обсуждение моделирования в общем как нормативного, основополагающего для жизни и возникающего из вычислений в живых системах ставит под сомнение некоторые все еще влиятельные идеи в западной философии. Одна из них — различие между «есть» и «должно» Дэвида Юма, которое стремится отделить описательные утверждения от нормативных. Юм отдавал предпочтение описанию, что было прогрессивной идеей в его время. Он считал, что описательные утверждения должны иметь приоритет над нормативными суждениями — и предшествовать им, иначе нам не было бы так раздражительно слышать мнения людей по темам, которые они не понимают. Для Юма факты («есть» утверждения) универсальны, в то время как мнения («должно» утверждения) являются лишь личными.

Хотя это интуитивно, дихотомия «есть/должно» распадается, когда мы осознаем, что модели не просто инертные матрицы чисел или платоновские идеи, плавающие в стерильной вселенной. Модели — это функции, вычисляемые живыми существами; можно утверждать, что они определяют живые существа. Таким образом, они всегда целенаправленны, присущи активному наблюдателю. Наблюдатели не являются безразличными сторонами. Каждое «есть» имеет неотъемлемую «должность». Наши умвельты таковы, каковы они, по вполне обоснованным причинам — длины волн, которые мы видим или не видим, категории, которые мы различаем или не различаем, переменные, которые мы считаем значительными или незначительными.

Подводя итог: Все знания или понимание мира зависят от наблюдателя; «Точное» лучше всего понимать как «полезное для предсказания будущего»; и «Полезное» можно интерпретировать как «хорошее для кого-то».

Философские «идеалисты», такие как Иммануил Кант (1724–1804), высказывали схожие аргументы, как и более современные постмодернистские философы и критические теоретики, которые выражают скептицизм относительно самой возможности независимых от наблюдателя утверждений «есть». В каком-то смысле они правы, но их солипсизм не обоснован.

Мы в основном можем согласиться на общую или «объективную» реальность, потому что все живем в одном и том же宇宙e. Внутри одного вида наши умвельты и, следовательно, наши модели — особенно касающиеся более физических аспектов окружающего мира — практически идентичны, если говорить статистически. Просто будучи живыми и взаимодействуя друг с другом, мы (в основном) соглашаемся соглашаться.

Платье, 2015

Редкость таких случаев, как Платье — интернет-феномен, ставший вирусным в 2015 году, — говорит о многом. Некоторые видят его белым и золотым, другие — синим и черным. Эта загадочная фотография кажется неоднозначной только потому, что была сделана при странном освещении; столкнувшись с самим предметом одежды, все соглашаются, что это на самом деле… как бы это ни было, я никогда не могу запомнить. То, как мы его воспринимаем, в значительной степени зависит от наших предыдущих ожиданий относительно освещения. Ранние пташки видят белое и золотое, в то время как совы (как я) видят синее и черное.

Иллюстрация того, как разные фильтры, соответствующие различным предположениям об освещении, приводят к различным интерпретациям цвета в Платье.

Даже между видами общий биологический инструментарий и взаимосвязанные умвельты, как правило, укрепляют консенсусную реальность. Наши интересы, а значит, и наши модели, все переплетены, будь то в сотрудничестве или противостоянии. На самом деле, порой трудно провести грань. Кролик, который не может эффективно распознать и отличить своих сородичей от волков, долго не продержится в этом мире. И волк, который не может распознать ужин, тоже. На протяжении эволюционного времени, через это, казалось бы, противостояние, волки и кролики сотрудничали, чтобы взаимно формировать тела друг друга и сложные модели мира.

Писатель-фантаст Филип К. Дик однажды написал: «Реальность — это то, что, когда ты перестаешь в нее верить, не исчезает».

Хотя сущность может игнорировать или по-разному интерпретировать многие из своих входных сигналов, неспособность понять связь между этими сигналами и своим будущим существованием приведет к будущему несуществованию. Таким образом, факты — это модели, которые работают достаточно хорошо, чтобы не убить вас.

Консенсус легче достичь для X, чем для H. Два агента, которые (возможно, благодаря тому, что оба являются людьми) обладают схожими сенсорными аппаратами, имеют общие инстинкты выживания, говорят на одном языке и смотрят на одно и то же платье, в подавляющем большинстве случаев согласуются в отношении его цвета.

С другой стороны, скрытое состояние H по определению недоступно для другого. Я могу сказать, что голоден или устал, или чувствую грусть, но… вам просто придется мне поверить. Или нет. В определенных обстоятельствах может быть важно, чтобы скрытые состояния оставались скрытыми. Поэтому мы начинаем беспокоиться, когда нейробиологи разрабатывают методы «чтения» скрытых состояний в нашем мозге, или когда компании социальных сетей пытаются использовать алгоритмическую магию, чтобы вывести наши самые сокровенные желания.

Являются ли чувства реальными? Самые элементарные виды чувств — это всего лишь физические сигналы: голод, холод, тепло, жажда. Для любого организма, стремящегося выжить — то есть для всего, что живо, поскольку оставаться живым требует постоянной работы — такие измерения имеют значение. Пришло ли время потеть или дрожать? Выберите неправильный ответ, и ваша модель может не остаться, чтобы делать какие-либо предсказания завтра.

Для бактерии такие измерения — это химические показатели, как и экологические переменные; они просто оценивают условия внутри клеточной мембраны, а не снаружи. Это подразумевает решение той же вычислительной задачи, что и для внешнего измерения. Найти корреляцию между сырым сигналом (например, событиями молекулярного связывания и расщепления) и оценочным свойством (например, концентрацией или голодом) требует обученной и, вероятно, адаптивной модели.

По мере усложнения организмов как механизмы сигнализации, так и модели, необходимые для определения переменной, такой как «голод», становятся более сложными.

Рассмотрим боль. В своей книге 2023 года «Машина опыта: как наш разум предсказывает и формирует реальность» философ Энди Кларк — с мнением которого о мозге как предсказателе я согласен — описывает множество показательных способов, которыми могут сбойнуть наши модели боли. Например, ампутанты могут испытывать фантомную боль в конечности. Аналогично, многие люди живут с хроническими болевыми расстройствами, которые часто начинаются с острого повреждения или болезни, но продолжаются долго после того, как физическое повреждение заживает.

С другой стороны, многие из нас знакомы с получением травм, иногда серьезных, которые не болят в начале — боль появляется позже, если вообще появляется, и иногда кажется, что она зависит от нашего более высокого уровня осознания травмы. Приведу один жуткий пример: в начале 2005 года строитель в Колорадо испытал то, что он воспринял как болезненный удар от рикошетящей гвоздезабивной машины на строительной площадке. Шесть дней спустя он посетил стоматолога, жалуясь на легкую зубную боль; он прикладывал лед и принимал «Адвил». Рентгеновский снимок показал, что он выстрелил четырехдюймовым гвоздем через небо рта и в свой мозг. Он хорошо восстановился после операции по удалению гвоздя, но эта газетная история не вдохновляет меня заниматься более сложными делами по дому.

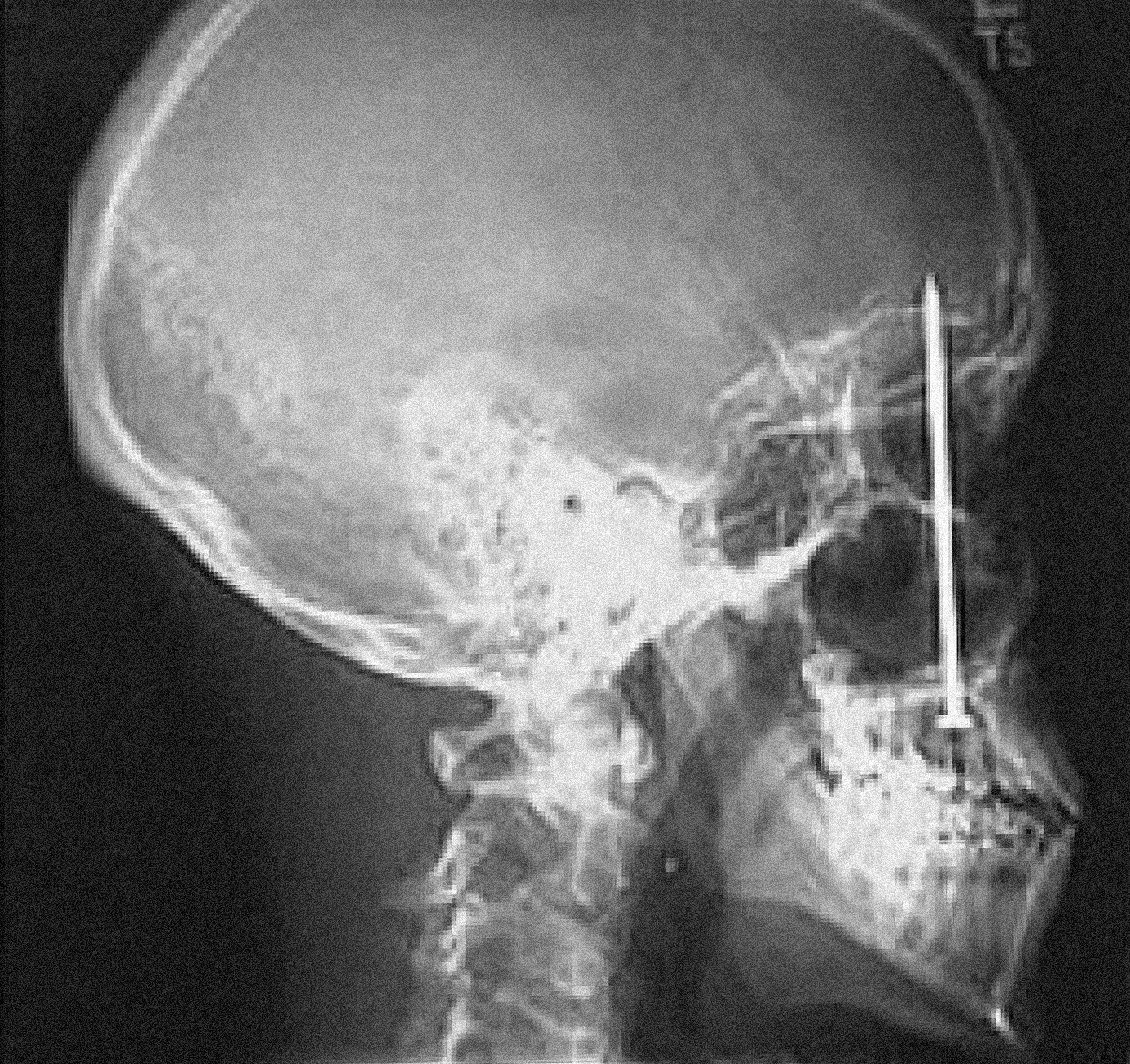
Рентгеновский снимок четырехдюймового гвоздя, вонзившегося в череп двадцатитрехлетнего строителя Патрика Лоулера, удаленного в больнице Литлтона в Денвере 14 января 2005 года, через шесть дней после того, как Лоулер неосознанно выстрелил в себя из гвоздезабивной машины.

Существует и противоположное явление, когда интенсивная боль сопровождает ошибочное восприятие травмы. Рассмотрим еще одну историю о несчастной встрече между строителем и гвоздем, как сообщалось в British Medical Journal в 1995 году.

Этот рабочий прыгнул с лесов на доску, не заметив выступающий семидюймовый гвоздь, который пробил его ботинок насквозь, выйдя сверху. В агонии строитель получил дозу фентанила и мидазолама. Но в приемном покое, когда врачи вытащили гвоздь и сняли ботинок, оказалось, что гвоздь прошел безвредно между его пальцами ног.

Ботинок двадцатидевятилетнего строителя, пробитый семидюймовым гвоздем, который, как оказалось в больнице, прошел безвредно между его пальцами ног, как сообщалось в
British Medical Journal
в 1995 году.

Как говорит Энди Кларк, «такие эффекты кажутся гораздо менее удивительными, как только мы принимаем, что […] ‘сырые’ сенсорные данные […] никогда не воспринимаются. […] [Р]еакции ‘рецепторов боли’ (известных как ноцицепторы) не являются тем, что мы чувствуем, когда нас охватывает острая боль. Вместо этого эти реакции — лишь один из источников доказательств […]. Вот почему мы можем искренне чувствовать боль, даже когда активность ноцицепторов отсутствует. Мы также можем не чувствовать боль, даже когда интенсивная активность ноцицепторов присутствует […]. То, что мы чувствуем […] отражает процесс бессознательной интерпретации […] событий, вызывающих наши сенсорные стимуляции.»

Точка зрения Кларка общая: дело не только в боли, но и в природе реальности, как внешней, так и внутренней, и в том, как эта «реальность» создается. За пределами различия «есть/должен» Хьюма, классическая и просветительская догма о том, что реальность можно четко отделить от психологии, ошибочна. Второй строитель не притворялся, что испытывает боль, так же как и первый строитель не делал вид, что ему не больно.

Ни Кларк, ни я не утверждаем, что реальность не существует. Скорее, мы используем «реальность» для описания целенаправленной модели с высокой степенью социального консенсуса и хорошей предсказательной силой.

Мы называем веру первого строителя в то, что он не получил травм, «ложной», потому что эта вера не предсказала бы драматичное рентгеновское исследование или срочную необходимость в операции. Мы называем веру второго строителя в его травму «ложной», потому что он ожидал, что, когда врачи снимут его ботинок, они обнаружат кровавую рану. Когда такой раны не оказалось, все поняли, что их модель нуждается в обновлении; и, в качестве бонуса, боль у мужчины исчезла.

К сожалению, это не всегда так просто. Для людей с хронической болью осознание того, что с ними ничего «не так», не приносит облегчения — так же, как для людей с арахнофобией сознательное знание о том, что домашний тарантул ручной, не избавляет от страха прикоснуться к этому гигантскому волосатому пауку.

Мы видели, как даже вирусу нужна оболочка, иначе он теряет способность существовать вне своей хозяинской клетки и становится транспозоном.

Читатели-математики: в первом приближении, если X — это последовательность дискретных событий, то в первом приближении P ( X ) будет причинным фильтром, превращающим эти дискретные события в непрерывную временную оценку вероятности. Элегантные компромиссы между точностью и задержкой, которые демонстрируют бактерии (по сути, изменяя форму фильтра), можно рассматривать как решение для оптимального линейного предсказания X в условиях меняющейся статистики.

Концепция «вещи самой по себе» ( Ding an sich ) происходит от Иммануила Канта, который стремился различить объективную реальность и наш неизбежно субъективный или «феноменальный» опыт ее восприятия. Хотя, чтобы немного опередить нашу аргументацию, как могла возникнуть эта невероятно стульяподобная конфигурация атомов в первую очередь, без существ, которые моделируют стулья?

Изначально Конвей использовал доску для го.

Го — это древняя стратегическая игра, изобретённая более 2500 лет назад в Китае, в которой два игрока по очереди ставят белые и чёрные камни на незанятые пересечения на сетке 19×19.

Техническое замечание: для моделирования квантовой механики также потребуется источник случайных чисел. Существует также вопрос начальных условий, о которых мы поговорим позже.

Это понимание или знание о мире Жизни согласуется с основными правилами и даже может быть выведено из них, так же как статистическая механика позволяет выводить температуру и давление из более низкоуровневых законов упруго сталкивающихся частиц в коробке (которые, в свою очередь, могут быть выведены из ещё более фундаментальной физики). Однако было бы странно утверждать, что глайдеры «подразумеваются» или «встроены» в правила Жизни, поскольку полнота Тьюринга Жизни означает, что сложность возможных конструкций в Жизни не ограничена; она включает в себя всё и вся.

Создавая систему нумерации, которая может перечислить все возможные клеточные автоматы, Стивен Вольфрам и его коллеги начали исследовать вопрос о том, насколько «необычными» являются вычисления в абсолютном смысле. Доказано, что правило номер 110 поддерживает вычисления — и многие из первых ста правил настолько тривиальны, что не создают никакой значимой динамики. Наблюдения подобного рода и простота Жизни Конвея предполагают, что вселенной не нужно быть настроенной с точностью, чтобы поддерживать вычисления.

Растения и грибы, формы жизни, лишённые мышц и поэтому движущиеся очень медленно, не следует воспринимать как пассивные. Напротив, как всё больше осознают учёные, изучающие их, они компенсируют свою неподвижность способностью совершать невероятное множество химических действий.

С технической точки зрения, самонаблюдение включает в себя преобразование незаслуженной задачи в заслуженную, каким-то образом помечая данные самими собой. Парадигматическим примером является предсказание следующего слова для обучения крупных языковых моделей.

Более формально, совместное распределение P(X, H, O) включает в себя «маргинальные распределения» P(H) и P(X), которые мы получаем, суммируя совместное распределение по (X, O) или (H, O), а также условные распределения.

Техническое примечание: как только эволюция «научилась» наделять организмы «первичными влечениями», такими как голод, она также может научиться использовать их в качестве внутренних оракулов для усиленного обучения и других, более сложных алгоритмов обучения, например, как описано в работе Керамати и Гуткина 2011. «Бутстрэппинг» в главе 4 объяснит усиленное обучение и его связь с мозгом более подробно.

Более формально, это требует уменьшения размерности распределения за счет выделения инвариантных размерностей, согласно Тишби, Перейре и Бялеку 2000.

Сжатый видеопоток 4K (3840×2160 пикселей) обычно составляет от восьми до четырнадцати миллионов бит в секунду. Это может показаться не таким уж значительным моделью, но этого достаточно для моделирования некоторых простых вещей, например, с отрицательным w — восстанавливающей силы, действующей при растяжении пружины на расстояние x.

Хотя различие не так просто, как кажется, как обсуждается в «Élan Vital» в главе 1.

Я написал версию для программистов с именами переменных в нижнем регистре, потому что в математической нотации заглавные буквы обычно используются для «случайных переменных», которые могут принимать целое распределение значений.

Хотя эта терминология немного запутанная, практики машинного обучения называют оценку своих обученных моделей «инференцией».

Отложив в сторону другие возможные формы жизни во Вселенной, мы находимся на грани того, чтобы это больше не было правдой на Земле, поскольку модели ИИ теперь используются для разработки других моделей ИИ, согласно Duéñez-Guzmán и др. 2023.

Эта мысль подсказывает потенциально плодотворное направление для исследований. Современные подходы к обучению, вдохновленные эволюцией, в основном основаны на случайных мутациях, согласно Salimans и др. 2017. Но, как мы видели, симбиогенез является гораздо более мощным источником продуктивной новизны.

«В общем» потому что преимущества групповой фитнеса возникают из индивидуальных жертв под определенными обстоятельствами, как, например, у пчел, защищающих улей. Также, в таких видах, как осьминог, где особи размножаются за один сезон и не участвуют в воспитании потомства, нет эволюционного давления на выживание после размножения.

Это альтернативная формулировка «Бритвы Оккама», которая утверждает, что при равных условиях более простое объяснение с большей вероятностью окажется истинным, чем сложное.

Уайт 1972. Примечание для физиков: возможно сформулировать физику в терминах «принципов наименьшего действия», а не эквивалентных динамических законов. Это потребует оценки всех возможных траекторий камня, чтобы найти решение с минимальным (или, иногда, максимальным) действием, при котором машина оказывается раздавленной. Можно утверждать, что в формулировке действия все эффекты предшествуют своим причинам, согласно Тегмарку 2018. Однако, на мой взгляд, устраняя любое представление о причинной последовательности, подход наименьшего действия предполагает вне-временной «блок-вселенную», где нет места таким понятиям, как «почему» и «потому что». Мы вернемся к этой теме в главе 6 «Будет то, что вы хотите».

Дикон 2012. В соответствии с расширением терминов, предложенным в «Élan Vital», глава 1, это определение «целеустремленного» или даже «живого» включает технологические системы с встроенными решениями, от термостатов до крылатых ракет, а также искусственно эволюционировавшие системы, такие как bff.

Хьюм 1817. Валлиш 2017. Дик 1985. Орловский 2020; Гёриг и др.

2021
↩
,
↩
.
A. Clark 2023
↩
.
KUSA-TV 2005; Nitsch, Verheggen и Merten 2007
↩
,
↩
.
Fisher, Hassan и O’Connor 1995; Zoffness 2024
↩
,
↩
.
A. Clark 2023
↩
.
интерлюдия
Предыстория вычислений