Глава 2.5: Интерлюдия

Предыстория вычислений

Вычисления могут быть основой жизни, интеллекта и всего остального, но их история полна извивов, ложных стартов и недопонимания. Чтобы лучше понять наши представления и заблуждения о вычислениях, нам нужно вернуться гораздо дальше, чем к Тьюрингу и фон Нейману, и связать их работы с корнями в математике, промышленной инженерии и нейронауке. Также необходимо учесть социальный контекст, в котором развивались эти идеи.

Это будет краткий и отобранный, а не окончательный или исчерпывающий рассказ. Его цель — переосмыслить наши устоявшиеся представления о том, что такое вычисления (или что это не является), и о их связи с мозгами и разумом, трудом, интеллектом и «рациональностью».

Наша предыстория вычислений начинается в эпоху европейского Просвещения с Готфрида Вильгельма Лейбница (1646–1716), соавтора исчисления и обладателя множества других достижений. Его «ступенчатая счетная машина» стала первым механическим калькулятором, способным выполнять все четыре основные арифметические операции, но это был лишь первый шаг в его гораздо более амбициозной программе.

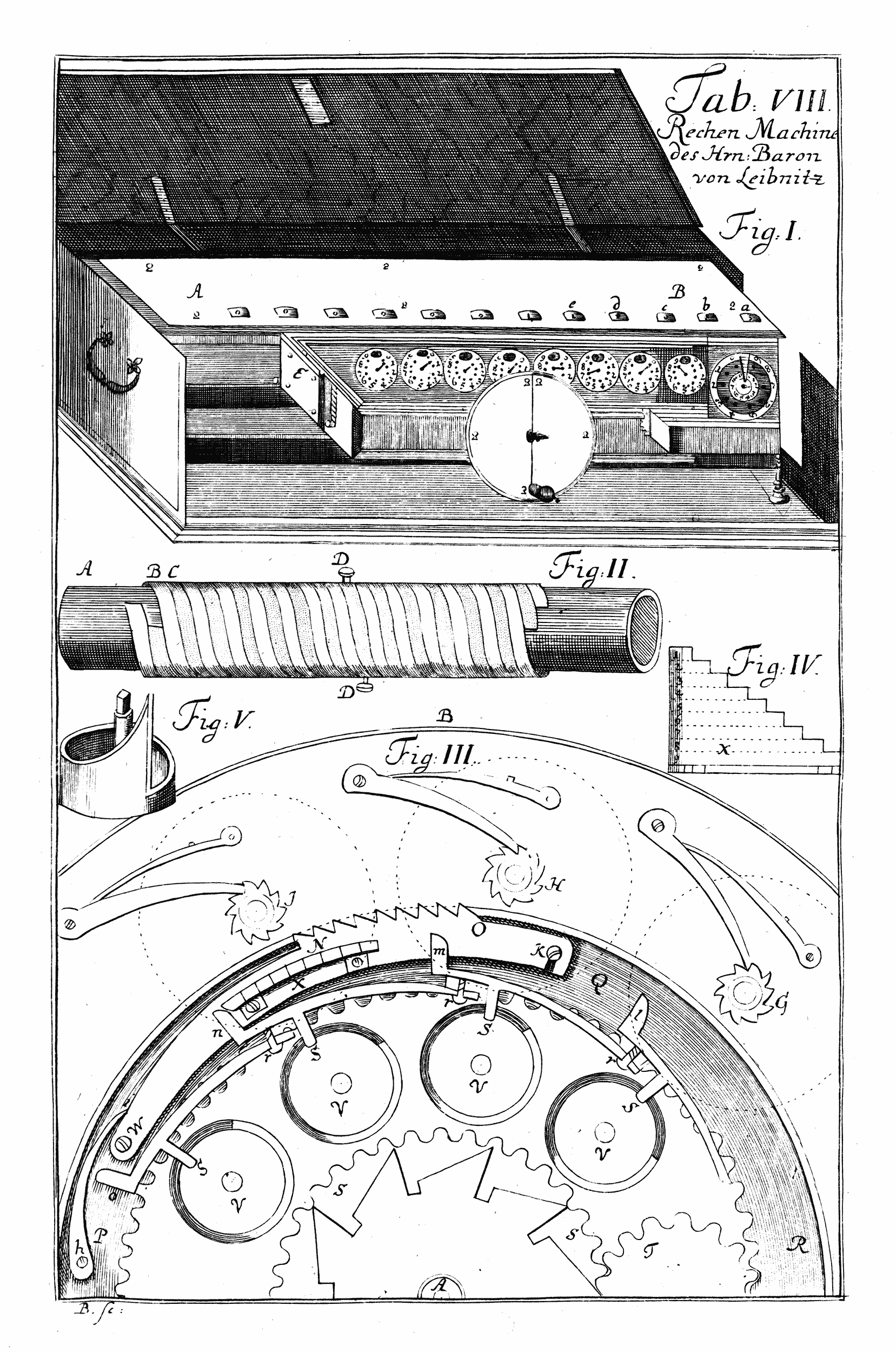
Посмертная схема ступенчатой счетной машины Лейбница, из Leupold 1727

В двадцать лет Лейбниц утверждал, что однажды мы сможем формулировать и отвечать на любой вопрос — не только в математике, но и в политике, экономике, философии, даже в этике или религии — используя чистую логику: «Если возникнут споры, не будет больше необходимости в диспутах между двумя философами, чем между двумя бухгалтерами. Достаточно будет взять в руки карандаши, сесть с планшетами и сказать друг другу […]: Давайте посчитаем [calculemus].»

Представляя, что бухгалтеры — по сути, человеческие компьютеры — смогут найти правильный ответ на любой вопрос, как только он будет правильно сформулирован, Лейбниц предполагал существование универсальной истины, как фактической, так и нормативной: платонического мира чистых, вне времени и аксиоматически верных идей.

Ему всего лишь нужно было разработать— или открыть— формальный язык для символического выражения любых предложений (он назвал это characteristica universalis, или «универсальная нотация»), и алгебру для манипулирования такими предложениями (a calculus ratiocinator или «калькуляция для рассуждений»). Существование Бога, право Габсбургов править Австрией и легитимность однополых браков можно было бы свести к логическим доказательствам, так же как и значение числа пи. И если это так, то потомок вычислительной машины в конечном итоге мог бы механически вычислять такие доказательства. Однако эта грандиозная идея медленно угасала на протяжении веков, хотя, в определенном смысле, вся область компьютерных наук выросла из её разлагающихся остатков, как молодое деревце из гнилого бревна. Не забывайте, что теоретические основы вычислений были заложены Тьюрингом в его попытке решить Entscheidungsproblem в 1930-х годах— задачу нахождения общего алгоритма для определения истинности математического утверждения. Это была проблема Лейбница, хотя и ограниченная математикой. Плохая новость: даже в этой чисто абстрактной, формальной области Тьюринг доказал, что такого алгоритма не существует. Хорошая новость: в процессе он изобрел (или открыл) универсальные вычисления. 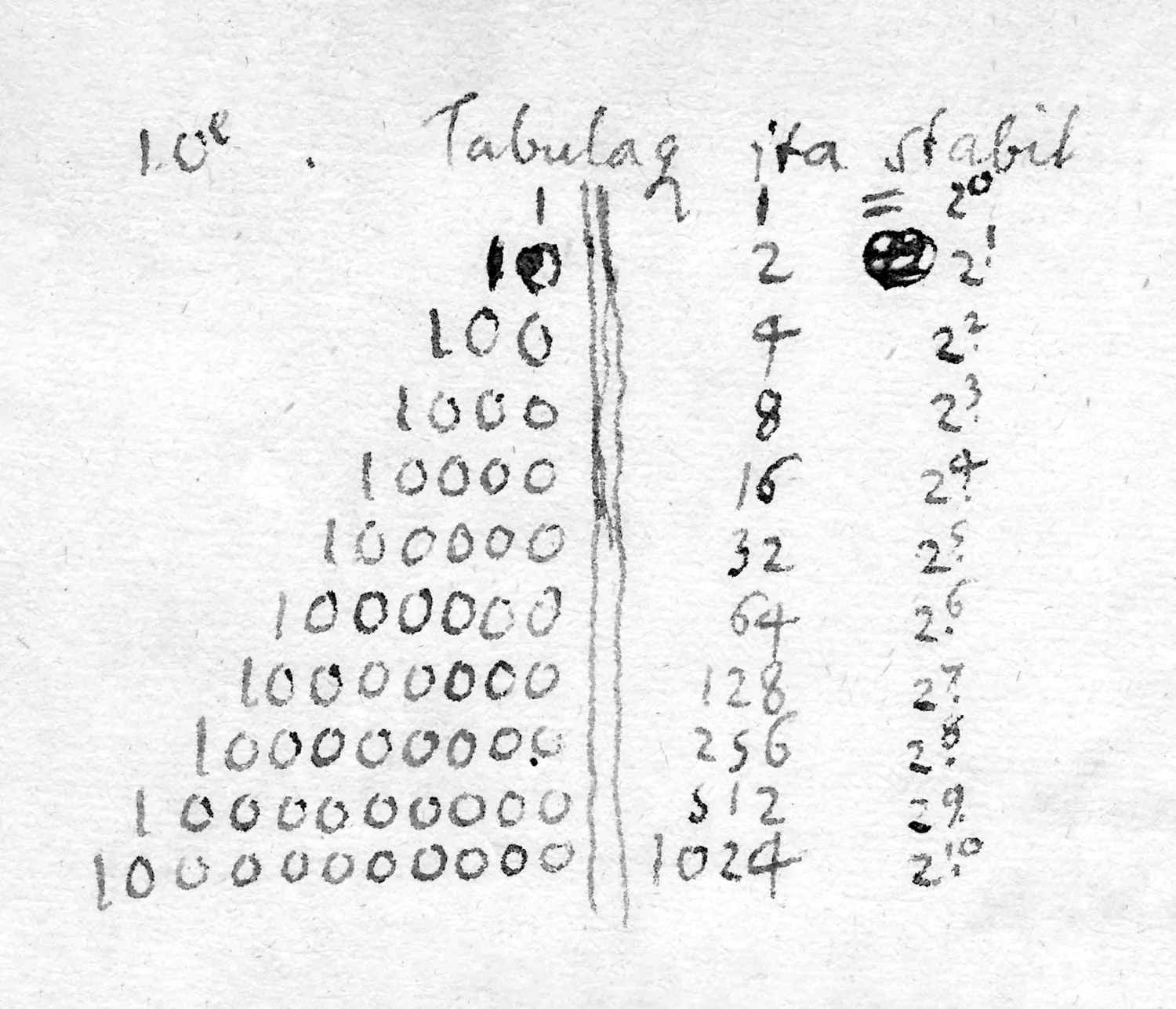Из рукописи Лейбница, около 1703 года Хотя Лейбниц работал над многими другими проблемами на протяжении своей долгой карьеры, он никогда не отказывался от поиска универсального символического языка. Это был его Святой Грааль. В новогоднем письме герцогу Брауншвейгскому в 1697 году Лейбниц с восторгом объяснял некоторые успехи на этом пути: числа можно было представлять в двоичном формате, используя только цифры 0 и 1. Письмо набросало дизайн медальона в честь этого открытия с изображением божественного творения, отмечая, что «трудно найти лучшее иллюстрацию этой тайны в природе или философии […] что Бог создал всё из ничего».
![Image](images/leibnizmedallion.

Дизайн медали Готфрида Вильгельма Лейбница 1697 года, посвященной двоичной нотации, изображает imago creationis («образ творения»), таблицу двоичных чисел от нуля до шестнадцати и девизы unum autem necessarium («один необходим») и unus ex nihilo omnia («один из ничего делает все»). Поскольку двоичная система была как минимальным представлением чисел, так и естественной нотацией для логики «да/нет», она казалась очевидной основой для characteristica universalis Лейбница. Джордж Буль (1815–1864), самоучка-математик девятнадцатого века, который формализовал булеву логику, лежащую в основе практически всех цифровых вычислений, независимо пришел к тому же выводу более чем через столетие.

Глупые прически ancien régime
Гаспар де Прони

На практике же первые «человеческие компьютеры» не использовали никакой специальной нотации и не решали сложные задачи на досках; другими словами, они не походили на философов-бухгалтеров Лейбница. Это были безработные парикмахеры, нанятые гражданским инженером Гаспаром де Прони (1755–1839), чтобы создавать книги таблиц логарифмических и тригонометрических функций для землемеров после Французской революции.
(Парикмахеры остались без работы, потому что многие из их прежних клиентов, аристократы Ancien Régime, теряли свои высокие прически, вместе с головами, под гильотиной. Выжившие, богатые и бедные, мудро предпочитали держать волосы короткими и простыми.) Эти парикмахеры, возможно, не знали высшей математики, но были привыкшими работать аккуратно и методично. Им не составляло труда выполнять элементарные операции, на которые было разбито каждое вычисление: сложение и вычитание.
Прони сформулировал свой проект в индустриальных терминах, хвастаясь, что разделение труда позволяет ему «изготавливать логарифмы так же легко, как производят булавки».

Ссылка на производство булавок пришла прямо из «Исследования о природе и причинах богатства народов» Адама Смита, основополагающего документа индустриального капитализма. Лейбниц жаловался, что «недостойно выдающихся людей тратить время на вычисления, когда любой крестьянин мог бы выполнить эту работу так же точно с помощью машины». Хотя парикмахеры Проня еще не использовали машины, они были организованы так, чтобы работать как одна. И, конечно, машины уже были изобретены для сложения и вычитания.

Гравюра булавочной фабрики из «Энциклопедии» Дидро и д'Аламбера, 1762 год, классическая иллюстрация разделения труда.

Проект Проня произвел большое впечатление на Чарльза Бэббиджа (1791–1871), создателя первого универсального компьютера, «Аналитической машины», в 1830-х годах. Полностью механическая, Аналитическая машина должна была работать на паровом двигателе и, вероятно, выполняла бы сложение за три секунды — гораздо медленнее любого электронного компьютера, но все же быстрее, чем вручную.

Хотя сегодня Бэббидж известен как несчастный изобретатель, опередивший свое время (ни Аналитическая машина, ни ее более скромный предшественник, «Машина разностей», не были построены при его жизни), он вовсе не был бездельником. На самом деле он был одним из великих архитекторов и теоретиков промышленной революции; его самая важная книга, «Об экономике машин и производств», была посвящена автоматизации фабрик. Она была полна практических инженерных и предпринимательских советов, собранных через тщательное наблюдение и подкрепленных данными о производительности.

▶
Реконструкция Машины разностей Бэббиджа №2 в Музее истории компьютеров в Маунтин-Вью, Калифорния.

Паровые компьютеры — это лишь одна (нехарактерно спекулятивная) идея среди многих в книге Бэббиджа.

Он ввел автоматическое вычисление в главе о разделении труда, отметив: «Действия г-на Проня в его знаменитой системе вычислений очень напоминают действия искусного человека, собирающего хлопковую или шелковую фабрику или любое подобное предприятие».

Кратко говоря, как и Пронь, Бэббидж стремился «изготавливать логарифмы». Механические вычисления были просто средством автоматизации работы парикмахеров Проня.

Параллель, которую провел Бэббидж с текстильными фабриками, красноречива, ведь его другим великим источником вдохновения был жаккардовый ткацкий станок, запатентованный Жозефом Мари Жаккардом в 1804 году. Машина Жаккарда сделала возможным массовое воспроизводство сложных узорчатых тканей, закодировав их дизайны в виде отверстий, пробитых в последовательности карточек. Похожие перфокарты должны были стать механизмом ввода и хранения данных для Аналитической машины.

▶ Жаккардовый ткацкий станок в музее Пейсли в Шотландии

Ада Лавлейс, семнадцать лет, 1832 год

В 1833 году баронесса Анна Байрон, реформатор образования и филантроп, привела свою семнадцатилетнюю дочь Аду, будущую графиню Лавлейс (1815–1852), на вечер в дом Бэббиджа.

Как вскоре написала леди Байрон: «Мы обе посетили машину мысли (так она кажется) в прошлый понедельник. Она возводила несколько чисел в 2-ю и 3-ю степени и извлекала корень квадратного уравнения. […] Там открывались возвышенные виды на конечные результаты интеллектуальной силы». Они стали свидетелями демонстрации работающего прототипа Разностной машины — столь же сложного компьютера, какой когда-либо увидит кто-либо из живущих тогда людей.

Несмотря на свой юный возраст, Ада Лавлейс (как ее обычно называют сегодня) понимала далеко идущие последствия этой машины. В последующие годы она стала интеллектуальным соратником Бэббиджа, когда незавершенная Разностная машина уступила место более грандиозным (и даже менее завершенным) планам для ее полностью программируемого преемника — Аналитической машины.

План Бэббиджа по созданию Аналитической машины
▶
Модель Аналитической машины Сидни Падуа

В 1842 году Лавлейс перевела лекцию итальянского военного инженера Луиджи Менабреа о Аналитической машине, добавив к ней серию заметок, которые были гораздо более объемными и проницательными, чем сама лекция. Заметка G содержит первую опубликованную компьютерную программу для Аналитической машины — следовательно, это первая опубликованная программа в принципе. Она вычисляла последовательности чисел Бернулли, которые часто встречаются в математическом анализе. Как знаменитая Лавлейс заметила: «Аналитическая машина плетет алгебраические узоры, так же как жаккардовый ткацкий станок создает цветы и листья».

Это наблюдение было даже более глубоким, чем кажется на первый взгляд, поскольку она, вероятно, понимала, что алгебраические узоры в настоящих цветах и листьях также создаются вычислительным образом, формируя математические закономерности лепестков, жилок, листьев и ветвей, обсуждаемые в главе 1.

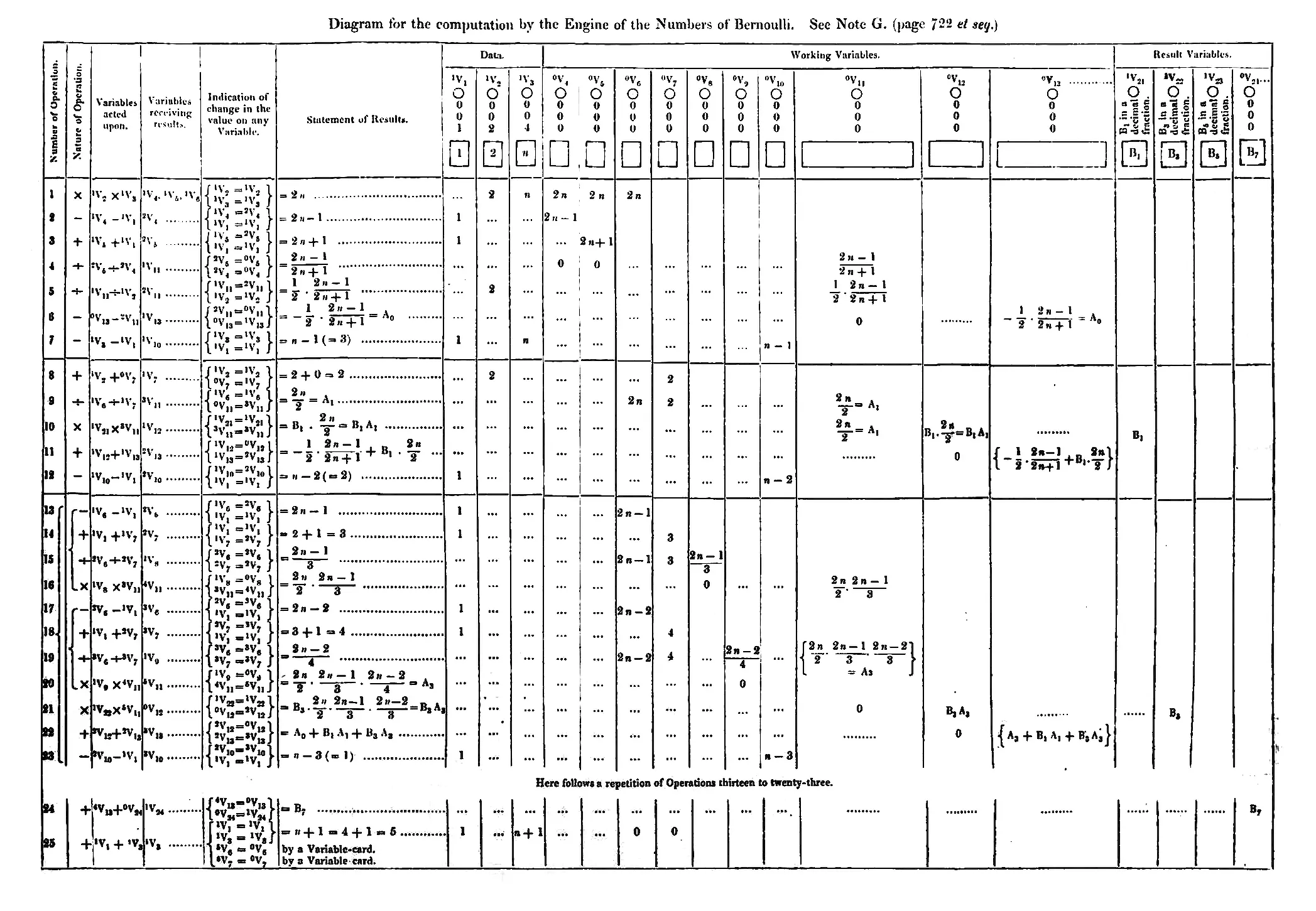
Программа Лавлейс для вычисления чисел Бернулли, из Заметки G к Эскизу Аналитической машины, 1842

Но до какой степени следует рассматривать компьютер как простой «ткацкий станок» для массового производства математических таблиц? Вычислительные машины Бэббиджа включали прекрасный дизайн принтера, способного создавать стереотипные пластины целых готовых страниц. Однако существует заметная разница между трудом, связанным с печатью таблиц (или производством булавок, или ткачеством ткани), и фактическим вычислением этих таблиц: первый вид труда является физическим, в то время как второй — умственным.

Surrey Comet, 1946

Это предполагает функциональную (а не только метафорическую) аналогию между компьютерами и мозгами. Эта аналогия широко использовалась журналистами на протяжении многих лет; например, в 1946 году газета Surrey Comet описала Автоматическую вычислительную машину Тьюринга (ACE) как «Электрический мозг, который будет создан в Теддингтоне».

Когда долгожданный ACE наконец был завершен в 1950 году, газеты вновь назвали его «электрическим мозгом», «электронным мозгом» или «машиной-умом». Мы склонны воспринимать такие заголовки как устаревший кликбейт, но это упускает из виду истинное понимание, стоящее за характеристикой Леди Байрон Разностной Машины как «мыслищей машины».

Вырезки из газет о Автоматическом Вычислительном Устройстве Тьюринга 1950 года

В наши дни мы предпочитаем термины вроде «обработка информации», чтобы избежать ассоциаций с сознанием и субъективным опытом, которые подразумевают слова «мышление» и «умственный», но стоит помнить, что для преданного индустриалиста, как Бэббидж, субъективность просто не имела значения. Насколько нам известно, он ни разу не задумывался над вопросом «каково это быть» механическим компьютером; впрочем, он также не беспокоился о том, «каково это быть» человеческим компьютером. Фабричная работа была чисто функциональной, действуя на уровне абстракции, превышающем индивидуальность — отсюда и взаимозаменяемость работников на конвейере. Как выразился Бэббидж: «[Д]еление труда можно с одинаковым успехом применять как к умственным, так и к механическим операциям».

Леди Байрон была воодушевлена «величием открывающихся перспектив конечных результатов интеллектуальной силы», но для других идея машин, выполняющих умственный труд, вызвала ранний проблеск тревоги, которую некоторые испытывают по поводу ИИ сегодня. В 1832 году, за год до встречи Лавлейса и Бэббиджа, Лондонский литературный вестник, возможно, лишь наполовину в шутку, назвал Бэббиджа «логарифмическим Франкенштейном». Умственная работа, возможно, еще не была значительным сектором рынка труда, но перспектива машин, способных «думать», все же вызывала определенное волнение.

▶
Голем, 1920
Насколько далеко могут продвинуться умственные функции механического монстра? По словам итальянского инженера Менабреа, «[Аналитическая машина] не является мыслящим существом, а просто автоматом, который действует в соответствии с установленными для него законами». Лавлейс согласилась, написав в своей заметке G: «Аналитическая машина не имеет никаких притязаний на то, чтобы что-либо создавать. Она может [только] выполнять то, что мы знаем, как ей приказать».
Это зомби-подобное изображение напоминает голема из средневекового еврейского фольклора: фигура из глины, оживленная могущественным раввином с помощью магических заклинаний — то есть кода. Голем может следовать командам, но без понимания и рассуждений.
Джордж Буль мог думать иначе. Напомним, что, как и Лейбниц, Буль верил в бинарную логику как универсальный калькулятор для рассуждений. Буль пошел дальше, утверждая, что это именно тот способ, которым мыслит разум; отсюда и название его великого трактата «Исследование законов мысли», опубликованного с большим успехом в 1854 году.
Предположительно, он имел в виду, что понимание и рассуждение сами по себе являются продуктами логики, поскольку, хотя Буль был религиозным, он (как и Лейбниц) считал логику и рациональность по своей сути божественными.
Человеческая душа была «рациональной душой», и наша субъективность проистекала из нашей рациональности, а не существовала вопреки ей.
В начале этот нейронаучный аспект тезиса Буля оставался в значительной степени незамеченным. Исключением стал друг и коллега Буля Август Де Морган (автор рифмы «У больших блох есть маленькие блохи» из главы 1), который сам работал над основами логики.
Викторианская интеллигенция была небольшим миром: Де Морган также был математическим наставником Ады Лавлейс и обучал ее математическому анализу и числам Бернулли.
Однако, в отличие от своих современников, Лавлейс не была удовлетворена выбором между логическими мозгами с одной стороны и мистическими неразъяснениями психических процессов с другой.

В письме к другу 1844 года — за десять лет до публикации «Законов мышления» Буля — Лавлейс написала: «Я надеюсь […] однажды получить такие церебральные феномены, которые смогу выразить в математических уравнениях; коротко говоря, закон или законы, описывающие взаимные действия молекул мозга […]. Главная трудность заключается в практических экспериментах».

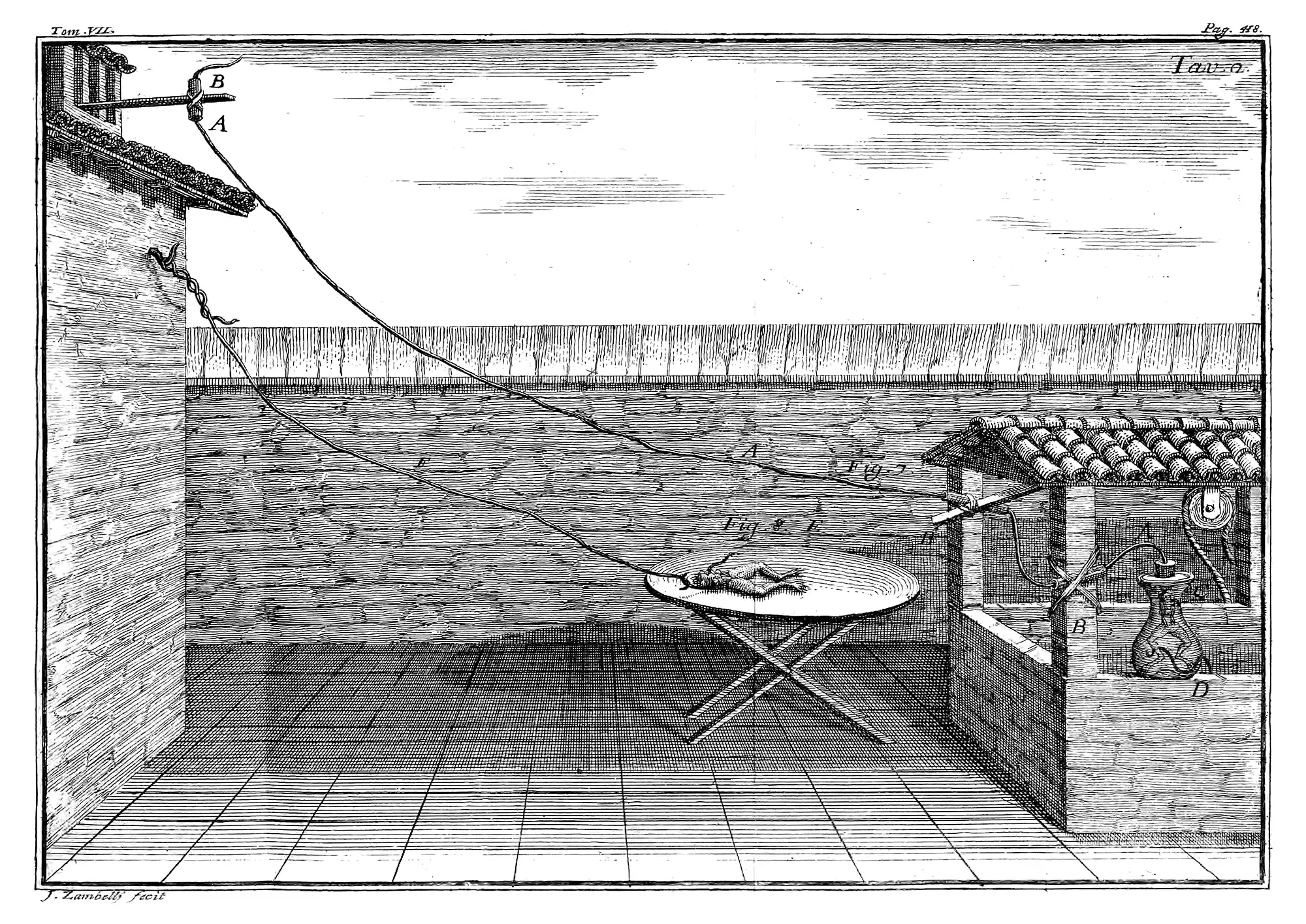
Электрофизиологические эксперименты Луиджи Гальвани

Электрофизиологические эксперименты Луиджи Гальвани

Электрофизиологические эксперименты Луиджи Гальвани

Электрофизиологические эксперименты Луиджи Гальвани

Лавлейс, безусловно, знала о сенсационных экспериментах Луиджи Гальвани (1737–1798). Гальвани обнаружил, что применение электрического тока к нервам свежезарезанных лягушек вызывает подергивание их лап. Племянник Гальвани, Джованни Альдини (1762–1834), продолжил его работу, легитимизируя свои исследования утверждениями — не совсем неправдоподобными — о том, что «галванические» шоки иногда могут вернуть к жизни утопленников и лечить душевнобольных. Современные дефибрилляторы и электрошоковая терапия являются наследниками этих ранних экспериментов.

Тем не менее, Альдини, похоже, был скорее шоуменом, чем ученым. В 1803 году он поспешил доставить повешенное тело осужденного Джорджа Фостера из Лондонской тюрьмы Ньютгейт в Королевский колледж хирургов для анатомической демонстрации. Согласно мрачному (и чрезвычайно популярному) «Календарю Ньютгейта», «при первом применении [электричества] к лицу покойного преступника его челюсти начали дрожать, а соседние мышцы ужасно искривились, и один глаз на самом деле открылся. В последующей части процесса правая рука была поднята и сжата в кулак, а ноги и бедра начали двигаться».

Гробовщик из Хирургической компании, как сообщается, вскоре после возвращения домой умер от страха.

Электрофизиологические эксперименты Джованни Альдини

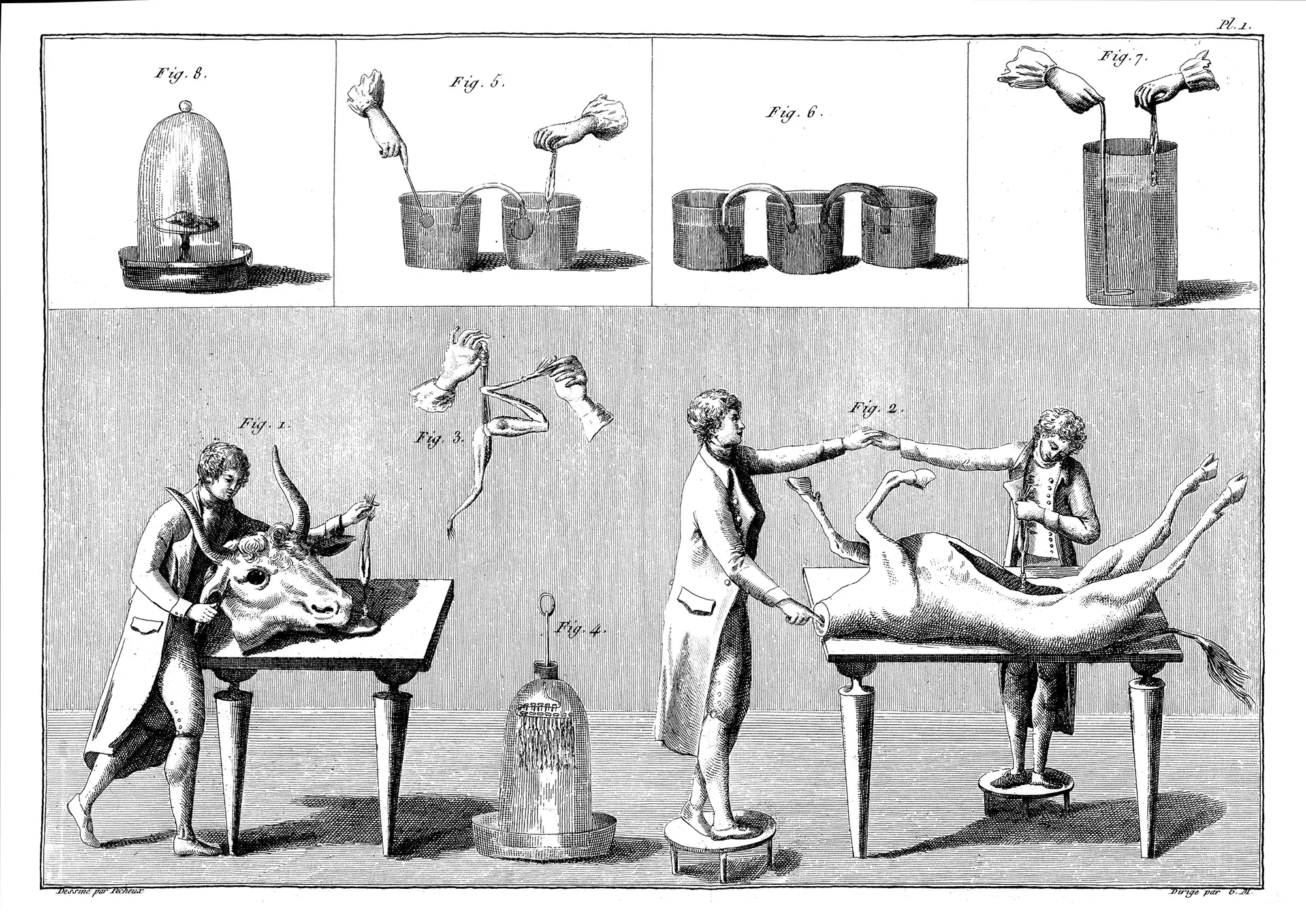
Электрофизиологические эксперименты Джованни Альдини

Электрофизиологические эксперименты Джованни Альдини

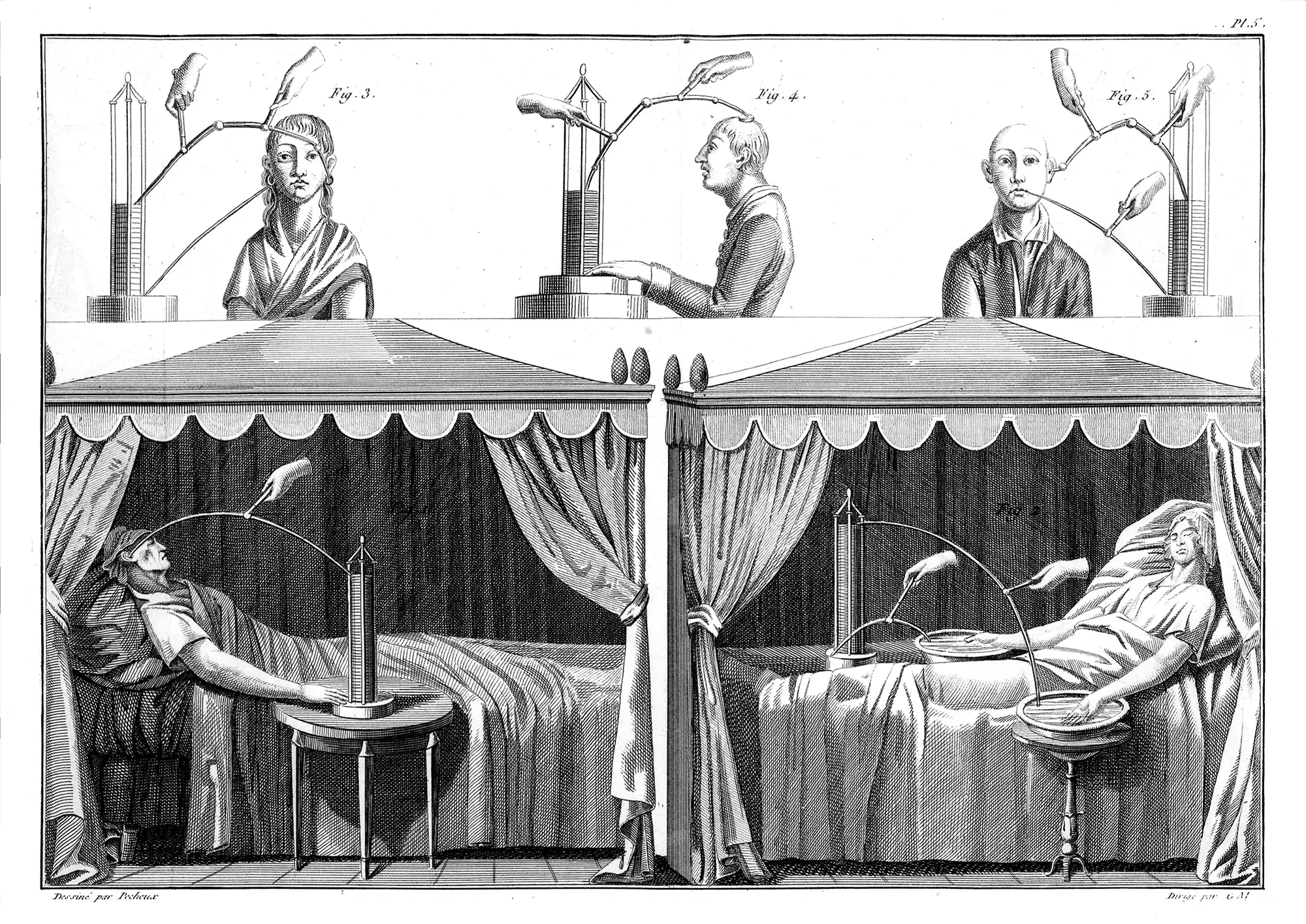
Электрофизиологические эксперименты Джованни Альдини

«Франкенштейн» Мэри Шелли, вероятно, был вдохновлен этими исследованиями. Возможно, под влиянием этого, Лавлейс написала, подчеркивая слова своим привычным энтузиазмом: «Я должна быть очень искусным практическим манипулятором в экспериментальных испытаниях; и это на материалах, с которыми трудно работать; а именно: мозг, кровь и нервы животных. […] Ни один из физиологов еще не нашел правильного пути; не могу понять, почему. […] Мне не кажется, что церебральное вещество должно быть более неуправляемым для математиков, чем звёздные и планетарные материи и движения, если бы они лишь взглянули на это с правильной точки зрения. Я надеюсь оставить потомкам «Калькуляцию Нервной Системы».»

Проводя параллель между нейронной активностью и ньютоновскими законами движения, Лавлейс подразумевала, что церебральный «калькуляс» не будет основан на абстрактной логике, как у Була и Аналитической Машины, а должен быть основан на эксперименте, и в этом она действительно была на правильном пути.

К сожалению, здоровье Лавлейс, всегда хрупкое, вскоре ухудшилось. Она начала принимать опиаты для борьбы с хронической болью и умерла через несколько лет, в возрасте тридцати шести лет, от рака матки. Мы никогда не узнаем, чего она могла бы достичь как нейрофизиолог или как первая вычислительная нейробиолог.

Когда реальные эксперименты с нервной тканью наконец начались, они сначала, казалось, подтверждали «цифровые» интуиции Лейбница и Була. В 1920-х годах пионер английской нейробиологии Эдгар Адриан начал электрически записывать «все или ничего» потенциалы действия, или «спайки», в сенсорных нейронах вскрытых лягушек в своей лаборатории в Кембридже.

Коллега и предшественник Адриана, Кит Лукас, уже установил, что импульсы в моторных нервных волокнах также действуют по принципу «всё или ничего».

Эдгар Адриан в лаборатории, около 1920 года

С учетом того, что нейронные входы и выходы, по-видимому, представляют собой бинарные электрические сигналы, идея о том, что мозг является логической машиной, выполняющей своего рода вычисления, получила мощную поддержку. В частности, если каждый нейрон имеет входы, соответствующие булевым единицам и нулям, и выдает булевый выход в ответ, то он становится логическим вентилем — то есть булевым оператором. И если это так, то активность мозга в целом будет представлять собой огромный логический расчет.

Две ключевые фигуры в современной нейронауке, Уоррен МаКаллок и Уолтер Питтс, объединили эти идеи в легендарной статье 1943 года «Логический расчет идей, присущих нервной активности». Это казалось осуществлением, девяносто девять лет спустя после письма Лавлейс, её задуманного «Калькулятора Нервной Системы»:

«Для психологии […] спецификация [нейронной] сети внесет все, что можно достичь в этой области — даже если анализ будет доведен до предельных психических единиц или ‘психонов’, ведь психон не может быть меньше, чем активность одного нейрона. […] Закон ‘всё или ничего’ этих активностей и соответствие их отношений логике высказываний гарантируют, что отношения психонов соответствуют двузначной логике высказываний. Таким образом, в психологии […] фундаментальные отношения — это отношения двузначной логики.»

Эта статья стала одновременно концом, началом и поворотным моментом — но не таким, каким его могли бы предвидеть её авторы. Как инженерный манифест, она оказала значительное влияние. Джон фон Нейман прочитал статью МаКаллоха и Питтса 1943 года как план того, как выполнять универсальные вычисления, используя электронные логические вентели вместо биологических нейронов (как упоминалось в главе 1).

В правильных конфигурациях эти ворота— сначала созданные с использованием вакуумных трубок, а позже транзисторов— могли бы реализовать Универсальную машину Тьюринга и, следовательно, вычислить что угодно. Булева архитектура была более минималистичной и элегантной, чем у Аналитической машины и её преемников, которые полагались на сложные механические компоненты и использовали десятичную арифметику.

Таким образом, можно рассматривать цифровые компьютеры как Универсальные машины Тьюринга, построенные из искусственно созданных нейронных сетей типа нейронов МакКаллоха и Питтса. Символы, используемые сегодня для обозначения логических ворот, были заимствованы непосредственно из графических изображений, которые МакКаллох и Питтс нарисовали для «пирамидальных нейронов» (которые, как следует из названия, имели форму пирамиды). Мы до сих пор рисуем маленький кружок на вершине пирамиды для логического отрицания (превращая AND в NOT-AND или NAND, OR в NOT-OR или NOR и так далее). Изначально этот кружок обозначал тормозной синапс, который, как считали МакКаллох и Питтс, реализует оператор NOT.

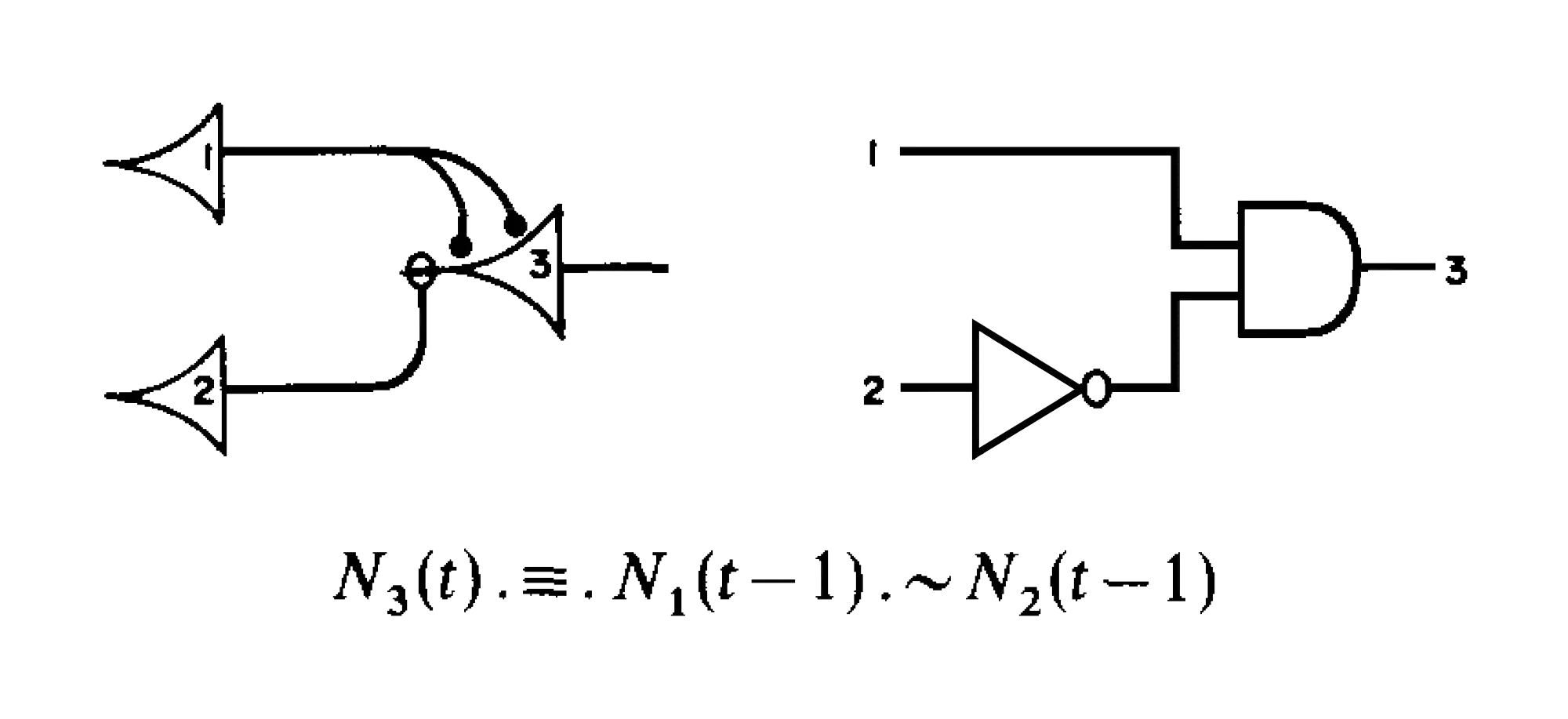
Слева: логическая схема из трех нейронов по МакКаллоху и Питтсу 1943 года (с их несколько неудобной нотацией для выполняемой логической операции ниже). Справа: эквивалентная схема с использованием современных символов логических ворот. Обратите внимание на формы нейронов и маленький кружок, представляющий операцию NOT, которую, как считали МакКаллох и Питтс, реализует тормозной синапс.

Несмотря на мощное влияние на компьютерную инженерию, как нейробиологическая теория, статья МакКаллоха и Питтса 1943 года оказалась ложным стартом. Она ознаменовала конец и высшую точку представления о том, что отдельные нейроны работают, выполняя логические операции. Нейробиологи послевоенного времени быстро установили, что хотя всплески напряжения «всё или ничего» действительно являются ключевым механизмом сигнализации в мозге, они не соответствуют логическим пропозициям, и нейроны не работают как логические ворота.

Также важны электрические поля и колебания более крупного масштаба; электрическая сигнализация не является единственной частью этой истории.

Богатство нейротрансмиттеров и нейромодуляторных химических веществ функционирует на различных уровнях — от локальной сигнализации с помощью специализированных «нейропептидов» до гормонов, выделяемых в кровь и влияющих на весь организм. Эти вещества играют ключевую роль в наших психических состояниях, эмоциях и мотивах. Появляющаяся картина остается вычислительной, но скорее в духе моделей Тьюринга для морфогенеза и «неорганизованных» нейронных сетей, нежели в каком-либо виде «вычислительного разума».

Тьюринг это понимал, как он ясно дал понять в своем выступлении на BBC Radio в 1951 году. Он согласился с утверждением Лавлейс о том, что написание программы привычным способом может привести лишь к предопределенному результату, похожему на голема — действительно, традиционное программирование включает в себя написание кода, функция которого полностью понятна программисту заранее, исключая любую возможность последующего поведения машины, которое можно было бы разумно назвать «творческим» или «интеллектуальным». Однако универсальность вычислений делает возможным реализацию любого вычислимого модели нейронной функции, включая «калькуляцию нервной системы» Лавлейс, на любой универсальной машине Тьюринга. Таким образом, Тьюринг сказал: «из этого следует, что наш цифровой компьютер, правильно запрограммированный, будет вести себя как мозг».

Хотя, как и Тьюринг, нейробиологи давно поняли, что мозг не является классической логической машиной, это сообщение долго не доходило до компьютерных ученых и исследователей ИИ. Напомним, что на протяжении всего двадцатого века многократные попытки ручного написания алгоритмов для выполнения самых простых повседневных задач, таких как распознавание изображений и речи, управление роботами и здравый смысл, полностью провалились, что привело к упомянутым в введении «зимам ИИ».

На протяжении многих десятилетий компьютеры могли выполнять логические задачи, которые считались чисто «механическими», с сверхчеловеческой скоростью, но, казалось, не могли справиться с повседневными «человеческими» задачами. Они не справлялись даже с задачами, которые многие другие животные с гораздо меньшими мозгами находят легкими.

Сначала стало казаться, что, несмотря на идеи Тьюринга о универсальных вычислениях, компьютеры могут иметь мало общего как с биологией, так и с мозгами.

1967 год, рекламная фотография актера Джонатана Харриса и робота из сериала «Потерянные в космосе», знаменитого фразой «не вычисляется».

Популярная культура искусственного интеллекта на протяжении двадцатого века пыталась преодолеть это очевидное несоответствие между мозгами и компьютерами, представляя, что когда — или если — ИИ наконец появится, он будет выдающимся в «рациональном» мышлении и логике, но слабым в человеческих эмоциях, креативности или здравом смысле. HAL 9000 и Дата из «Звёздного пути» — яркие примеры этого.

Сообщение было таково: компьютеры могут выполнять рутинные вычисления уже сегодня и, возможно, в будущем превзойдут людей в «академических знаниях», но, будучи подобными големам, они совершенно не похожи на нас; человеческий дух не поддается логике и рациональности. Мы не можем быть сведены к простым вычислениям.

Этот троп кажется особенно привлекательным для Голливуда, вновь и вновь появляясь в таких франшизах, как «Терминатор», «Робокоп» и «Матрица». Если Буль был мыслителем эпохи Просвещения, живущим в романтический период, то Голливуд по-прежнему полон скрытых романтиков, живущих в постмодернистскую эпоху.

Что привлекает нас к такому человеческому эксепционализму? Частично на этот вопрос можно ответить и самому; конечно, нам нравится думать о себе как о чем-то fundamentally отличном, лучшем в каком-то неколичественном смысле, обладающим неким «je ne sais quoi», который навсегда останется вне досягаемости надвигающегося «другого». Национальности и этнические группы постоянно играют в эту идентификационную игру.

Однако, помимо очевидного, нарратив о «неизмеримо человеческом» является утешительным, потому что Промышленная революция установила вычислительную иерархию, в которой бездушные, механические задачи выполнялись на самом низком уровне организационной структуры своего времени — сначала женщинами, затем машинами, которые их заменили — чтобы джентльмены-ученые из высшего общества могли быть освобождены для более разнообразных, творческих и интеллектуальных занятий, которые они считали достойными названия «умных».

Как отмечает историк науки Джессика Рискин, «Наше понимание того, что такое интеллект, изменялось в зависимости от того, что мы могли заставить делать машины, но одновременно наше представление о том, на что способны машины, изменялось в соответствии с тем, что мы считали интеллектом. […] Первые эксперименты по автоматизации были посвящены определению ее высших пределов, что одновременно означало выявление низших пределов человечности».

Сегодня мы сталкиваемся не только с тем, что эти пределы продолжают смещаться, но и с тем, что они упрямо отказываются выстраиваться в правильной последовательности согласно нашим классовым предвзятостям. Сегодня легче представить себе, что врача заменяет модель ИИ, чем медсестру. Мы, вероятно, не увидим ИИ-сантехников в ближайшее время, но ИИ-физики (по крайней мере, ИИ-ассистенты по физике) могут появиться очень скоро. Когда большие языковые модели могут читать и подводить итоги сложным аргументам, писать эссе и стихи, создавать программное обеспечение и так далее, очевидная иерархия информационных задач, где компьютер может заменить только работу плохо оплачиваемых или необразованных, перестает существовать. ИИ больше не является, как это описывал Лейбниц, «искусственными крестьянами», производящими логарифмы.

ИИ также не является чисто «умным» супернёрдом, каким его представляли в СМИ двадцатого века. Настоящий ИИ не обязательно чрезмерно логичен; на самом деле, его неудачи в решении логических задач или даже простых арифметических проблем стали важной темой критики ИИ в начале 2020-х годов.

Теперь недостаток компьютерной логики воспринимается как признак отсутствия интеллекта!

Современный ИИ, как инженерная дисциплина, тоже является разрушительным; он мало связан с языками программирования, структурами данных и парадигмами, которые еще совсем недавно были основой факультетов компьютерной инженерии. Модели ИИ могут работать на универсальных машинах Тьюринга, но они не являются алгоритмами в классическом смысле. Вместо этого они решают задачу моделирования вероятностных распределений напрямую из данных.

Так откуда же пришел новый подход к вычислениям и ИИ? Как оказывается, он был здесь все это время, просто не в мейнстриме. Понимание этой альтернативной концепции и ее связи с другими дисциплинами требует следования по другому пути, отличному от пути Лейбница, Буля и традиционной информатики — пути, вдохновленному живыми системами, который воспринимал вычисления не столько через призму логики, сколько через призму обучения и предсказания.

Это был путь кибернетики, идея которой начала развиваться еще в 1940-х годах, в военное время, и уже к 60-м годам начала терять свою популярность.

Более подробные истории часто начинаются с механизма Антикиферы — механического астрономического компьютера, найденного на затонувшем корабле в Эгейском море, который, как предполагается, датируется II веком до нашей эры. Многие ранние цивилизации производили астрономические и календарные расчеты, будь то для навигации, сельского хозяйства или религиозных ритуалов. Если под «компьютером» мы понимаем нечто, созданное для помощи в таких расчетах, то древние археологические памятники, построенные для выравнивания с солнцем, планетами и звездами, также могут считаться таковыми.

Роберт Гук из Королевского общества остался не впечатлён: «Что касается арифметического инструмента, который был представлен здесь перед этим обществом, то он показался мне настолько сложным с колесами, шестернями, пружинами, винтами, стопорами и катками, что я не мог представить, что он когда-либо будет иметь какую-либо значительную пользу».

Эта цитата из Б. Рассела 1937 года.

Самым влиятельным математиком конца девятнадцатого и начала двадцатого века был Давид Гильберт (1862–1943), который в 1920-х годах поставил проблему решения (Entscheidungsproblem) в центр своей программы по формализации математики.

Лейбниц не был первым и единственным математиком, открывшим бинарную систему; как и в случае с почти каждым значительным открытием или изобретением, это было сделано рядом других мыслителей примерно в то же время, включая Томаса Хериота (1560–1621), Фрэнсиса Бэкона (1561–1626) и Хуана Карамуэля и Лобковица (1606–1682). См. Глазер 1971 ↩ .

По словам Мэри Эверест Бул, «Джордж позже узнал, с великой радостью, что та же концепция основы логики была присуща Лейбницу […]». М. Э. Бул 1901 ↩ .

Это также совпало с ранним энтузиазмом по поводу метрической системы, которая стремилась вытеснить устаревшие «иррациональные» и аристократически окрашенные системы измерений. К сожалению для Проня, метрический подход к углам (сто градаций для прямого угла, вместо девяноста градусов) так и не прижился, что сделало многие таблицы бесполезными. Граттан-Гиннесс 1990; Гриер 2007 ↩ , ↩ .

Согласно Бэббиджу 1832 ↩ , «[Э]ти люди, как правило, оказывались более точными в своих расчетах, чем те, кто обладал более обширными знаниями по предмету». А. Смит 1776 ↩ .

Мартин 1992 ↩ .

Эти классовые и гендерные несправедливости, конечно, будут бесконечно повторяться в последующие века. Бромли 1982 ↩ .

Бэббидж 1832 ↩ .

По словам Бэббиджа 1864 ↩ , «Для тех, кто знаком с принципами жаккардового ткацкого станка и также знаком с аналитическими формулами, общее представление о средствах, с помощью которых Машина выполняет свои операции, может быть получено без особых трудностей». На самом деле, жаккардовые перфокарты использовались широко для обработки данных и вычислений вплоть до 1980-х годов.

Отец Лавлейс был печально известным романтическим поэтом, лордом Байроном; ее родители прожили вместе менее года из-за нестабильности и скандального образа жизни лорда Байрона (включая, как опасалась леди Байрон, инцестуальные отношения с его сводной сестрой).

Часть этого прототипа сохранилась и сейчас находится в Научном музее в Лондоне. Разностная машина, как и многие специализированные вычислительные машины первой половины двадцатого века, не была полным Тьюрингом; она могла лишь табулировать ограниченный (хотя и полезный) набор функций, используя «метод разностей» (математические любители: дискретная версия полиномиального ряда).

Лавлейс и Менабреа 1842

Числа Фибоначчи тесно связаны с числами Бернулли; см. Byrd 1975.

Surrey Comet 1946. Ранее специализированные компьютеры также регулярно назывались подобным образом, наиболее известным из которых был «Старый латунный мозг» — долговечный механический компьютер для предсказания приливов, изобретенный в 1895 году и использовавшийся Геодезической службой США с 1910 по 1965 год.

Национальная физическая лаборатория 1950.

Бэббидж 1832.

Лондонская литературная газета и журнал красивых искусств, наук и т.д. 1832; Шелли 1818.

Лавлейс и Менабреа 1842. В своем отчете 1948 года о «Интеллектуальных машинах» Тьюринг назвал это «Возражением леди Лавлейс» к идее о том, что машины могут быть интеллектуальными.

Г. Буль 1854.

Лабат 2024.

Согласно его вдове, Мэри Эверест Буль, в письме 1901 года: «почти все логики и математики проигнорировали утверждение о том, что книга предназначена для прояснения природы человеческого разума; и воспринимали формулу исключительно как замечательный новый метод упорядочивания логически массы доказательств о внешних фактах […]. Де Морган, конечно, понимал формулу в ее истинном смысле; он был соавтором Буля на протяжении всего времени». М. Э. Буль 1901.

Гальвани 1791; Альдини 1804.

Кнапп и Болдуин 1826.

Шелли 1818.

Письмо от 15 ноября 1844 года, написанное в Эшли Комбе, к Воронцову Грейгу, российскому послу в Лондоне. Лавлесс 1992
↩
.
«Сенсация возникает от сообщений, которые передаются через нервы от органов чувств к мозгу [...]. [Э]ти сообщения [...] состоят из [...] кратких импульсов в каждом нервном волокне; все импульсы очень похожи, независимо от того, предназначено ли сообщение для возбуждения ощущения света, осязания или боли.» Адриан 1928
↩
.
Лукас и Адриан 1917
↩
.
Основные логические операторы принимают два входа и выдают один выход; это AND, OR и XOR (сокращение от «eXclusive OR»). AND выдаёт единицу только в том случае, если оба входа равны единице, и ноль в противном случае; OR выдаёт ноль только если оба входа равны нулю, и единицу в противном случае; XOR выдаёт единицу, если один и только один вход равен единице. Оператор NOT с одним входом инвертирует своё значение, выдавая единицу, если вход равен нулю, и ноль, если вход равен единице. Комбинации этих операторов могут быть использованы для создания любой более сложной логической функции.
Маккалох и Питтс 1943
↩
.
Компьютер Harvard Mark I, задуманный Говардом Айкеном в 1937 году и построенный в 1940-х, был тесно смоделирован на Аналитической машине, включая её зависимость от десятичной арифметики. После 1943 года практически все электронные компьютеры использовали двоичную систему.
Как уже упоминалось, все пионеры вычислительной техники сделали шаг от логических машин, предназначенных для выполнения конкретной вычислительной задачи, к программируемым универсальным машинам, которые, будучи построенными, могли выполнять закодированные инструкции для выполнения любой вычислительной задачи — эквивалентно универсальной машине Тьюринга. Это и было различие между Разностной машиной Бэббиджа и Аналитической машиной. Это также было различие между фиксированными вычислительными машинами, созданными до 1945 года, и теми, что появились после, при этом ENIAC стал мостом между этими эпохами.

(ЕНИАК изначально был компьютером с фиксированной функциональностью, который требовал «программирования» путем переподключения его соединительных панелей, но к 1947 году он был обновлен и стал полностью программируемым с помощью программного обеспечения.) Агера и Аркас, Фэрхолл и Бялек 2000 ↩ . С. Дж. Смит и др. 2020 ↩ . Тьюринг 1951 ↩ . Хаугеланд 1985 ↩ . Ричардс и Лилликрап 2022 ↩ . Кларк 1968 ↩ . Хотя, что любопытно, они считали само собой разумеющимся, что компьютеры вскоре смогут распознавать лица и объекты, понимать речь и выполнять множество других повседневных задач, которые оказались столь же сложными. Возможно, эти задачи казались слишком простыми, слишком неинтересными с точки зрения повествования или просто слишком незначительными, чтобы служить основой для человеческого исключительства. Такие иерархии интеллекта уходят корнями еще дальше — к Декарту и даже к Аристотелю — но индустриальное производство сделало эту иерархию еще более буквальной. Риски 2003 ↩ . Кибернетика